Distance entre un point et une ligne

Vous trouverez ici la formule utilisée pour calculer la distance entre un point et une ligne. De plus, vous pourrez voir plusieurs exemples et exercices résolus de distances entre points et lignes et, même, les applications que cette opération a (par exemple, trouver la distance entre des lignes parallèles).

Formule pour la distance entre un point et une ligne

La distance entre un point et une ligne est la distance la plus courte entre ce point et la ligne. Mathématiquement, cette distance minimale est équivalente à la longueur du segment tiré du point à la droite et qui est perpendiculaire à la droite.

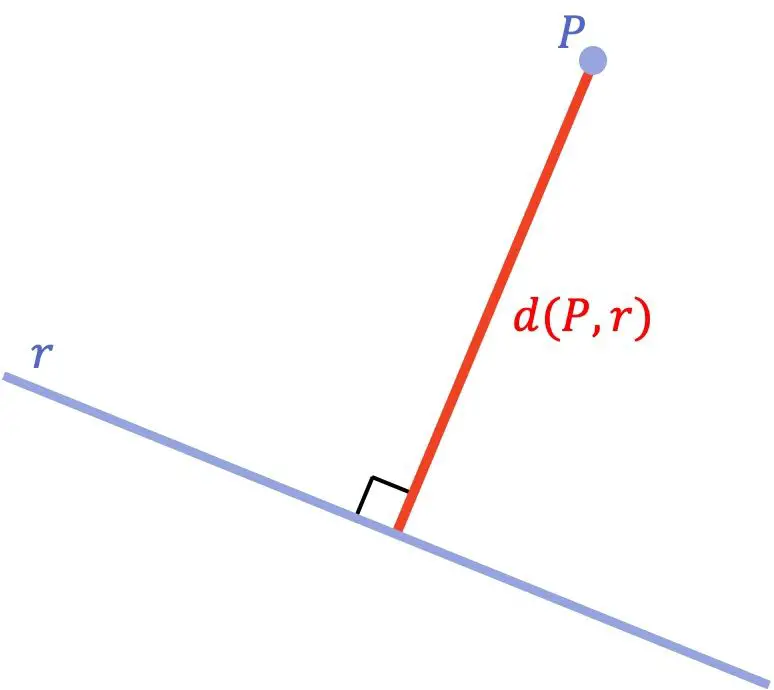
quelle est la distance entre un point et une droite

Une fois que nous avons vu le concept géométrique de distance entre un point et une ligne, voyons quelle est la formule utilisée pour calculer ladite distance :

Étant donné l’équation implicite (ou générale) d’une droite et les coordonnées de n’importe quel point d’un plan :

$r: \ Ax+By+C=0 \qquad \qquad P(p_x,p_y)$

La formule de la distance entre un point et une droite est :

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Important: notez que l’équation de la ligne dans la formule est sous la forme d’une équation implicite (ou générale), donc, si nous avons la ligne exprimée dans un autre type d’équation, nous devons d’abord la passer à son équation implicite et ensuite nous pouvons appliquer la formule.

Exemple de calcul de la distance entre un point et une ligne

Ci-dessous, vous pouvez voir un exemple de calcul de la distance entre un point et une ligne :

Trouver la distance entre le point $P$ et le droit $r:$

$P(2,-1) \qquad \qquad r: \ 3x+4y-5=0$

Pour calculer la distance entre le point et la droite, il suffit d’appliquer sa formule :

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Maintenant, nous remplaçons chaque terme par sa valeur :

$d(P,r)= \cfrac{\lvert 3\cdot 2 + 4\cdot (-1)-5\rvert}{\sqrt{3^2+4^2}}$

Et enfin on calcule la distance :

$d(P,r)= \cfrac{\lvert 6 -4-5\rvert}{\sqrt{9+16}} =\cfrac{\lvert -3 \rvert}{\sqrt{25}} = \mathbf{\cfrac{3}{5}}$

Distance entre deux lignes parallèles

L’une des applications du calcul de la distance entre une ligne et un point est de trouver la distance entre des lignes parallèles.

Évidemment, pour comprendre le concept que nous expliquerons ci-dessous, vous devez savoir ce que sont les lignes parallèles , donc si vous ne connaissez pas exactement leur définition, nous vous laissons un lien où nous l’expliquons en détail et vous pourrez également voir des exemples de lignes parallèles.

Pour trouver la distance entre deux lignes parallèles, il suffit de prendre un point sur l’une des deux lignes et de calculer la distance de ce point à l’autre ligne.

Ainsi, pour déterminer la distance entre deux lignes parallèles, la formule de la distance entre une ligne et un point est également utilisée.

D’autre part, si lors de l’utilisation de la formule, nous obtenons une distance de 0 unités, cela signifie que les lignes se touchent à un moment donné et, par conséquent, les lignes ne sont pas parallèles, mais se croisent, coïncident ou perpendiculaires. Si vous le souhaitez, vous pouvez vérifier les différences entre ce type de lignes sur notre site Web.

Voyons donc comment résoudre un problème de distance entre deux droites parallèles à travers un exemple :

Trouvez la distance entre les deux droites parallèles suivantes :

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

La première chose que nous devons faire est d’obtenir un point sur l’une des lignes (celle que vous voulez). Dans ce cas, nous allons calculer un point sur la droite

$s.$ Pour cela il faut donner une valeur à une des variables, on fera par exemple $x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

Et maintenant, nous effaçons l’autre variable (

$y$ ) de l’équation obtenue pour savoir combien il vaut à ce point :

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Par conséquent, le point obtenu à partir de la droite

$s$ est:

$P(0,-2)$

Et une fois que nous avons déjà un point sur une ligne, nous calculons la distance de ce point à l’autre ligne en utilisant la formule :

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{2}{\sqrt{20}}=\bm{0,45}$

Problèmes résolus de distance entre un point et une ligne

Exercice 1

Calculer la distance entre le point

$P$ et le droit $r:$

$P(4,2) \qquad \qquad r: \ 5x-3y+6=0$

voir solution

Pour trouver la distance entre un point et une droite, il suffit d’appliquer sa formule :

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Nous remplaçons chaque terme par sa valeur et calculons la distance :

$d(P,r)= \cfrac{\lvert 5\cdot 4 + (-3)\cdot 2+6\rvert}{\sqrt{5^2+(-3)^2}}=\cfrac{20}{\sqrt{34}}= \bm{3,43}$

Exercice 2

Quelle est la distance entre le point

$P$ et le droit $r$ ?

$P(-3,-1) \qquad \qquad r: \ y=-3x+5$

voir solution

Dans ce cas, l’équation de la droite est sous forme implicite (ou générale). Au lieu de cela, pour utiliser la formule de la distance d’un point à une ligne, la ligne doit être exprimée sous la forme d’une équation implicite. Il faut donc d’abord transformer la droite et la passer à une équation implicite (il suffit de passer tous les termes du même côté de l’équation) :

$r: \ 3x+y-5=0$

Et une fois que la ligne est déjà sous forme explicite, nous pouvons maintenant utiliser la formule de la distance entre un point et une ligne :

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Nous substituons donc chaque terme à sa valeur et calculons la distance :

$d(P,r)= \cfrac{\lvert 3\cdot (-3) + 1\cdot (-1)-5\rvert}{\sqrt{3^2+1^2}}=\cfrac{\lvert -9-1-5\rvert}{\sqrt{9+1}}=\cfrac{15}{\sqrt{10}}= \bm{4,74}$

Exercice 3

Quelle est la distance entre les deux lignes suivantes ?

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

voir solution

Tout d’abord, nous allons vérifier qu’il s’agit de deux droites parallèles. Pour cela, les coefficients des variables

$x$ et $y$ doivent être proportionnels entre eux mais pas aux termes indépendants :

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

En effet, les droites sont parallèles, on peut donc appliquer la procédure.

Maintenant, nous devons obtenir un point de l’une des lignes (celle que vous voulez). Dans ce cas, nous allons calculer un point sur la droite

$s.$ Pour cela il faut attribuer une valeur à une des variables, on fera par exemple $x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

Et maintenant, nous effaçons l’autre variable (

$y$ ) de l’équation obtenue pour connaître sa valeur en ce point :

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

De sorte que le point obtenu à partir de la ligne

$s$ est:

$P(0,-1)$

Une fois que nous connaissons un point sur une ligne, nous calculons la distance de ce point à l’autre ligne avec la formule :

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

Exercice 4

Calculer la valeur de l’inconnu

$k$ de sorte que la distance entre le point $P$ et le droit $r$ soit 5 unités.

$P(-2,5) \qquad \qquad r: \ 12x-5y+k=0$

voir solution

Il faut d’abord appliquer la formule de la distance entre un point et une droite :

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Maintenant, nous remplaçons chaque terme par sa valeur et simplifions l’expression :

$d(P,r)= \cfrac{\lvert 12\cdot (-2) + (-5)\cdot 5+k\rvert}{\sqrt{12^2+(-5)^2}}= \cfrac{\lvert -24-25+k\rvert}{\sqrt{169}}=\cfrac{\lvert -49+k\rvert}{13}$

L’énoncé du problème nous dit que la distance entre le point et la droite doit être égale à 5, donc on égale l’expression précédente à 5 :

$\cfrac{\lvert -49+k\rvert}{13}=5$

Et on résout l’équation résultante. Dans le numérateur de la fraction il y a une valeur absolue, donc, il faut analyser séparément quand la valeur absolue est positive et quand elle est négative :

$\cfrac{+(-49+k)}{13}=5$