Sur cette page vous trouverez tout sur l’équation de la circonférence : équation ordinaire, équation générale, autres types d’équations de la circonférence, quand l’équation d’une circonférence est correcte,… De plus, vous verrez des exemples de comment trouver l’équation d’une circonférence et vous pourrez vous entraîner avec des exercices résolus.
Équation ordinaire du cercle
Avant de voir ce qu’est l’équation de la circonférence, rappelons la notion de circonférence :
La circonférence est le lieu des points du plan équidistants d’un point fixe appelé centre.

Par conséquent, tous les points d’un cercle sont à la même distance de son centre.
De plus, le cercle est l’une des quatre sections coniques avec l’ellipse, la parabole et l’hyperbole. Autrement dit, un cercle peut être obtenu en coupant un cône avec un plan parallèle à sa base.
La façon la plus simple de décrire un cercle dans le plan cartésien est à partir de son équation ordinaire. Ainsi, la formule de l’équation ordinaire de la circonférence est la suivante :
L’ équation ordinaire du cercle est :
![]()
Où:
 est le rayon du cercle.
est le rayon du cercle. et
et sont les coordonnées du centre du cercle :
sont les coordonnées du centre du cercle :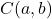
Bien que nous n’en fassions pas la démonstration car elle est un peu fastidieuse, cette équation peut être obtenue à partir du théorème de Pythagore.
Voyons comment l’équation ordinaire d’un cercle est calculée avec un exemple :
- Déterminer l’équation ordinaire du cercle de rayon 5 dont le centre est le point
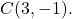
La formule de l’équation ordinaire d’un cercle est :
![]()
Par conséquent, nous n’avons qu’à substituer l’inconnu
![]() par la valeur du rayon, et les inconnues
par la valeur du rayon, et les inconnues![]() et
et![]() par les coordonnées X et Y respectivement du centre du cercle :
par les coordonnées X et Y respectivement du centre du cercle :
![]()
Donc l’équation ordinaire du cercle est :
![]()
Équation générale du cercle
Un autre type d’équation de circonférence est l’équation générale, en fait, c’est la plus utilisée. Nous allons voir ensuite comment obtenir l’équation générale de toute circonférence à partir de son équation ordinaire.
Soit l’équation ordinaire d’un cercle :
![]()
Si on développe les égalités remarquables (ou produits remarquables) :
![]()
![]()
Maintenant on fait 3 changements de variables :
![]()
Et enfin on obtient l’équation générale de la circonférence :
![]()
La formule de l’ équation générale de la circonférence est donc :
![]()
où le centre du cercle est :
![]()
Et le rayon du cercle vaut :
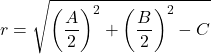
Donc cette équation de la circonférence s’obtient toujours par l’équation ordinaire. Voici un exemple pour voir comment c’est fait :
- Déterminer l’équation générale du cercle de rayon 6 dont le centre est le point
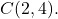
Il faut d’abord trouver l’équation ordinaire du cercle. Pour ce faire, nous utilisons sa formule :
![]()
![]()
Et maintenant on opère jusqu’à trouver l’équation générale de la circonférence, c’est-à-dire jusqu’à ce qu’on ne puisse plus simplifier :
![]()
![]()
![]()
![]()
Donc l’équation générale du cercle est :
![]()
Bien que le problème ne le demandait pas, nous pouvons maintenant calculer le centre et le rayon de l’équation trouvée pour vérifier qu’elle est correcte.
Pour déterminer le centre du cercle, nous utilisons sa formule :
![]()
![]()
![]()
![]()
En effet, le centre du cercle coïncide avec celui de l’énoncé.
On vérifie aussi le rayon de la circonférence avec sa formule :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04dc99d462a8ceb5e6dca936999a4ce8_l3.png)
Et le rayon est également égal à celui de l’énoncé. Par conséquent, l’équation de la circonférence calculée est correcte.
Existence d’une circonférence
Toutes les équations sous la forme de
![]() correspondent à un cercle. Ainsi, pour que ce type d’expression soit véritablement l’équation d’un cercle, les 3 conditions suivantes doivent être remplies :
correspondent à un cercle. Ainsi, pour que ce type d’expression soit véritablement l’équation d’un cercle, les 3 conditions suivantes doivent être remplies :
- Les coefficients de
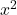 et de
et de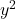 ils doivent être égaux à 1. Gardez à l’esprit que si les deux variables étaient précédées d’un nombre autre que un mais qu’elles avaient toutes deux le même nombre, l’équation entière pourrait être divisée par ce nombre afin que leurs coefficients soient 1.
ils doivent être égaux à 1. Gardez à l’esprit que si les deux variables étaient précédées d’un nombre autre que un mais qu’elles avaient toutes deux le même nombre, l’équation entière pourrait être divisée par ce nombre afin que leurs coefficients soient 1. - L’équation ne peut pas avoir de terme
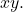
- L’expression suivante doit être positive :
![]()
Autres types d’équations du cercle
Les deux équations du cercle que nous avons vues, l’équation ordinaire et l’équation générale, sont les plus utilisées pour exprimer mathématiquement un cercle dans le plan (en R2). Cependant, il existe plusieurs types d’équations pour décrire cet objet géométrique, ci-dessous l’explication de chacun d’eux.
Équation canonique du cercle
L’équation canonique, ou équation réduite, d’un cercle sert à décrire tout cercle dont le centre est à l’origine des coordonnées , c’est-à-dire au point (0,0). Ladite équation est la suivante :
![]()
Si, en plus, le rayon était équivalent à l’unité (1), l’équation de la circonférence serait :
![]()
Cette dernière équation correspond à la circonférence goniométrique, également appelée circonférence unitaire ou cercle unitaire. C’est le cercle de rayon 1 centré sur l’origine des coordonnées.
Équations de deux cercles concentriques
Deux équations concentriques sont celles qui ont le centre au même point. Et la seule chose différente que deux cercles concentriques ont est le rayon.
Donc, pour que cette condition soit remplie, les équations de deux cercles concentriques sont exactement les mêmes à l’exception de leurs termes indépendants, qui doivent être différents.
![]()
![]()
Par exemple, les deux cercles suivants sont concentriques, puisque tous leurs coefficients sont identiques sauf les termes indépendants :
![]()
![]()
Équation paramétrique du cercle
Comme la ligne, l’équation d’un cercle peut également être paramétrée avec les fonctions trigonométriques du sinus et du cosinus. Ainsi, les équations paramétriques du cercle sont :
![Rendered by QuickLaTeX.com \diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)](https://mathority.org/wp-content/ql-cache/quicklatex.com-72dae5b3c5f775661ecb102945bb3fbd_l3.png)
où le point
![]() est le centre du cercle et
est le centre du cercle et![]() c’est votre rayon.
c’est votre rayon.
Problèmes résolus de l’équation d’un cercle
Exercice 1
Calculer l’équation générale du cercle de rayon 5 dont le centre est au point
![]()
Pour trouver l’équation générale du cercle, il faut d’abord trouver son équation ordinaire. Pour ce faire, on utilise la formule de l’équation ordinaire d’un cercle :
![]()
![]()
![]()
Une fois que l’on connaît l’équation ordinaire, on opère jusqu’à trouver l’équation générale du cercle :
![]()
![]()
![]()
![]()
Donc l’équation générale du cercle est :
![]()
Exercice 2
Pour chacun des cercles suivants, trouve les coordonnées de son centre et la longueur de son rayon.
![]()
![]()
![]()
circonférence A)
![]()
La circonférence s’exprime sous la forme d’une équation ordinaire, dont la formule est :
![]()
Par conséquent, les coordonnées du centre du cercle sont :
![]()
![]()
Et son rayon vaut :
![]()
![]()
circonférence B)
![]()
Cette circonférence s’exprime sous la forme d’une équation générale, donc pour calculer les coordonnées de son centre il faut utiliser la formule suivante :
![]()
![]()
![]()
![]()
D’autre part, la formule pour trouver le rayon du cercle est :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0cdc38937e6c36bb9e6d2ca0814a650_l3.png)
circonférence C)
![]()
La circonférence s’exprime sous la forme d’une équation ordinaire, dont la formule est :
![]()
Par conséquent, les coordonnées du centre du cercle sont :
![]()
Dans ce cas, l’équation n’a pas de terme.
![]() ni
ni![]() il est donc centré sur l’origine des coordonnées :
il est donc centré sur l’origine des coordonnées :
![]()
Et son rayon vaut :
![]()
![]()
Exercice 3
Laquelle des équations suivantes est l’équation d’un cercle ?
![]()
![]()
![]()
![]()
Pour qu’une expression soit l’équation d’un cercle, les conditions suivantes doivent être vraies :
1. Les coefficients de
![]() et de
et de![]() Ils doivent être égaux à 1.
Ils doivent être égaux à 1.
2. L’équation ne peut pas avoir de terme![]()
3.![]()
Nous devons donc vérifier que les trois conditions sont remplies pour chaque équation.
Équation A)
![]()
Les coefficients de
![]() et
et![]() sont 1 et l’équation n’a pas de terme
sont 1 et l’équation n’a pas de terme![]() Il suffit donc de vérifier la troisième condition :
Il suffit donc de vérifier la troisième condition :
![]()
![]()
![]()
![]()
![]()
L’équation vérifie les 3 conditions, c’est donc l’équation d’un cercle.
Équation B)
![]()
L’équation a un terme avec
![]() avec lequel l’équation ne correspond pas à un cercle.
avec lequel l’équation ne correspond pas à un cercle.
Équation C)
![]()
Les coefficients de
![]() et
et![]() ne sont pas 1, mais on peut transformer l’équation en divisant tous les termes :
ne sont pas 1, mais on peut transformer l’équation en divisant tous les termes :
![]()
De cette façon maintenant les coefficients de
![]() et
et![]() oui ils sont 1 et, de plus, l’équation n’a pas de terme
oui ils sont 1 et, de plus, l’équation n’a pas de terme![]() Nous n’avons donc qu’à corroborer la troisième condition :
Nous n’avons donc qu’à corroborer la troisième condition :
![]()
![]()
![]()
![]()
![]()
L’équation vérifie les 3 conditions, c’est donc l’équation d’un cercle.
Équation D)
![]()
Les coefficients de
![]() et
et![]() sont 1 et l’équation n’a pas de terme
sont 1 et l’équation n’a pas de terme![]() Il suffit donc de vérifier la troisième condition :
Il suffit donc de vérifier la troisième condition :
![]()
![]()
![]()
![]()
L’équation ne satisfait pas la dernière condition, donc ce n’est pas l’équation d’un cercle .
Exercice 4
Déterminer l’équation du cercle passant par les trois points suivants :
![]()
L’équation générale de tout cercle est :
![]()
Par conséquent, nous devons substituer les coordonnées des points dans l’équation du cercle pour trouver les paramètres
![]()
![]() et
et![]()
Avec le premier point de on trouve le coefficient
![]()
![]()
Avec le deuxième point on trouve le coefficient
![]()
![Rendered by QuickLaTeX.com \begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-12719654d98ba81f0a7d45e587478e6d_l3.png)
Et à partir du troisième point, nous trouvons le coefficient
![]()
![Rendered by QuickLaTeX.com \begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f1e69c28996a8fbfa14189c48a295095_l3.png)
En conclusion, l’équation générale de la circonférence est :
![]()
Exercice 5
Si les extrémités opposées d’un cercle sont les deux points suivants :
![]()
Quelle est l’équation ordinaire du cercle ?
Si les deux points sont les extrêmes du cercle, son centre sera le milieu entre ces deux points :
![]()
![]()
![]()
D’autre part, le diamètre du cercle sera la distance entre les deux points, qui peut être calculée à l’aide de la grandeur du vecteur que forment les deux points :
![]()
![]()
Et le rayon du cercle est la moitié du diamètre :
![]()
L’équation ordinaire du cercle est donc :
![]()
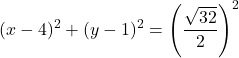
![]()
Enfin, si cet article vous a été utile, vous serez sûrement également intéressé par nos pages hyperbole (mathématiques) et parabole (mathématiques) . Vous y trouverez une explication détaillée de ce que sont l’hyperbole et la parabole, leurs équations, leurs caractéristiques, des exemples, des exercices résolus…