Parabole (mathématiques): définition, équation, éléments, exemples,…

Sur cette page vous trouverez tout sur la parabole : qu’est-ce que c’est, ce qu’elle représente, ses éléments (foyer, directrice, sommet, etc.) son équation (avec les différents types d’équations de la parabole), des exemples, des exercices résolus, ses propriétés, ses applications,…

Qu’est-ce qu’une parabole ?

La parabole est un concept qui a des significations très différentes, mais sa définition mathématique est la suivante :

En mathématiques, une parabole est le lieu des points du plan qui sont équidistants d’un point fixe (appelé le foyer) et d’une ligne fixe (appelée la directrice).

Par conséquent, tout point d’une parabole est à la même distance de son foyer et de sa directrice.

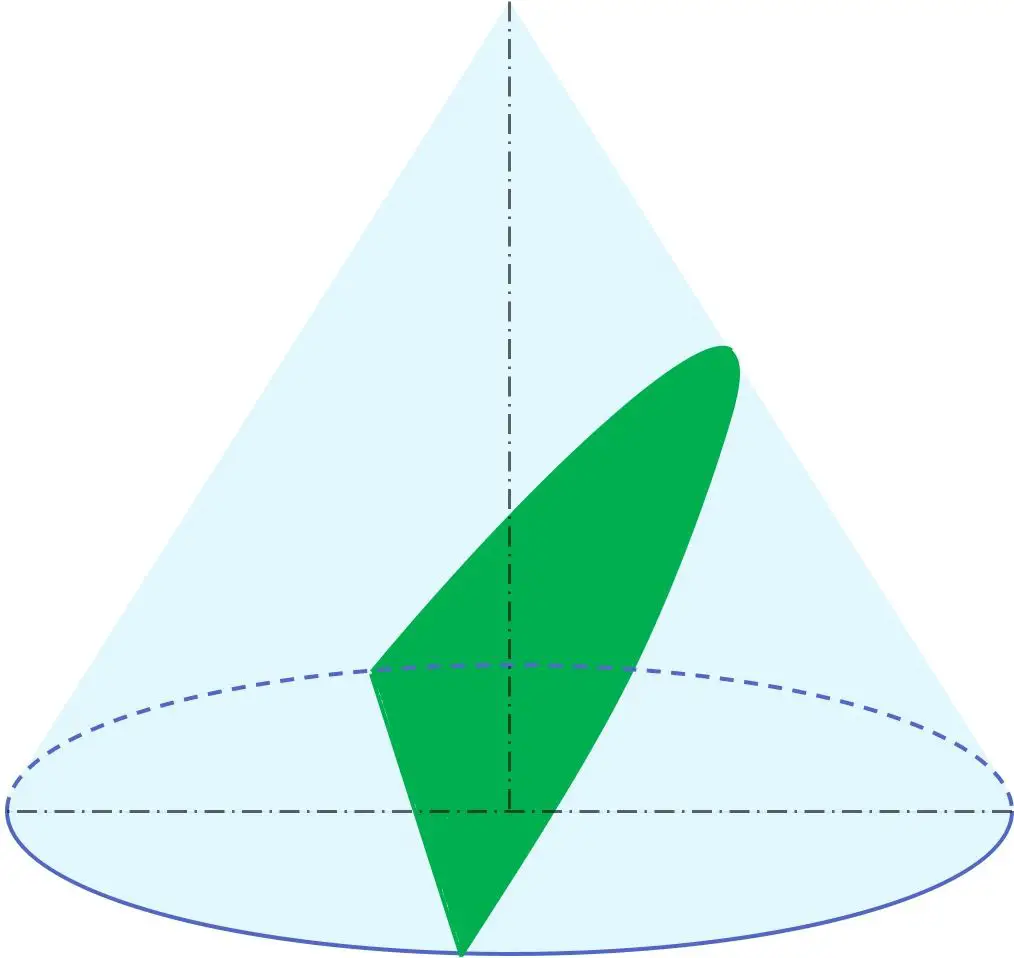
De plus, en géométrie, la parabole est l’une des sections coniques avec la circonférence, l’ellipse et l’hyperbole. Autrement dit, une parabole peut être obtenue à partir d’un cône.

En particulier, la parabole résulte de la coupe d’un cône par un plan d’angle d’inclinaison par rapport à l’axe de révolution équivalent à l’angle de la génératrice du cône. Par conséquent, le plan contenant la parabole est parallèle à la génératrice du cône.

Éléments d’une parabole

Les caractéristiques d’une parabole dépendent des éléments suivants :

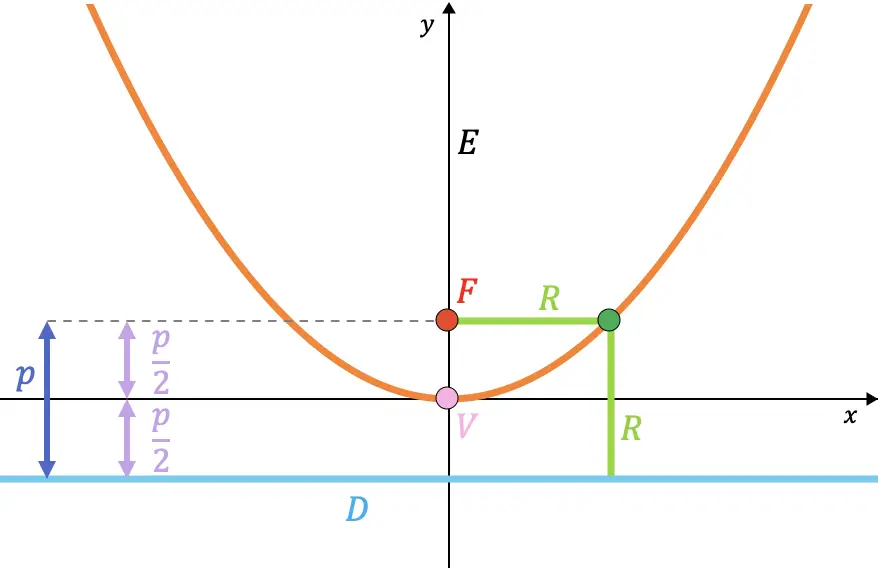
Foyer (F) : est un point fixe à l’intérieur de la parabole. La distance de n’importe quel point de la parabole au foyer est égale à la distance de ce même point à la directrice de la parabole.
Directrice (D) : c’est une droite fixe extérieure à la parabole. Un point de la parabole est à la même distance de la directrice que du foyer de la parabole.
Paramètre (p) : est la distance du foyer à la directrice.
Vecteur rayon (R) : est le segment qui joint un point de la parabole au foyer. Sa valeur coïncide avec la distance du point à la directrice.
Axe (E) : est la droite perpendiculaire à la directrice qui passe par le foyer et est l’axe de symétrie de la parabole, dans le graphique ci-dessous elle correspond à l’axe des ordonnées (axe Y). Aussi appelé axe focal.
Vertex (V) : est le point d’intersection entre la parabole et son axe.
Distance focale : est la distance entre le foyer et le sommet, ou entre la directrice et le sommet. Sa valeur est toujours égale à $\displaystyle \frac{p}{2}.$

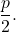
côté droit

Le côté droit d’une parabole est la corde à l’intérieur de la parabole qui passe par le foyer et est parallèle à la directrice.

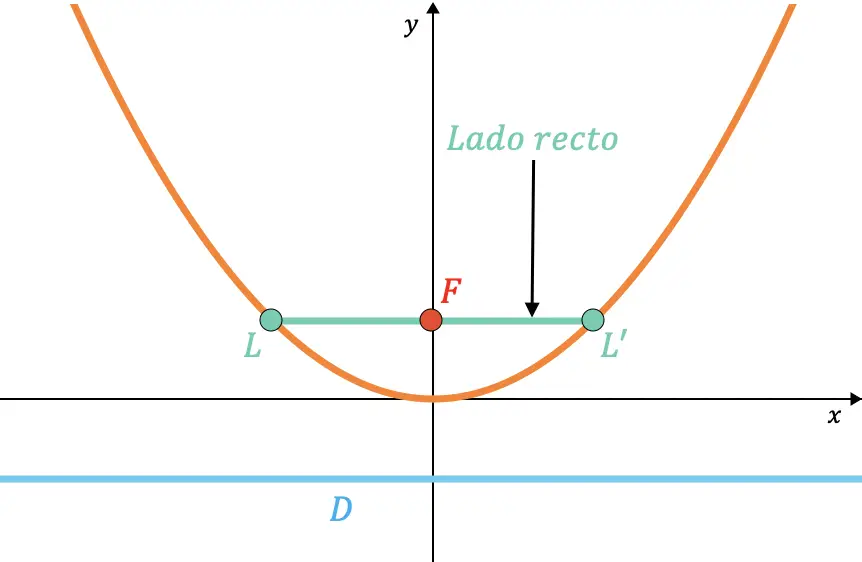
De même, on peut montrer que la longueur du côté droit est toujours le double de la valeur du paramètre

$p.$

$\lvert LL'\rvert = 2p$

D’autre part, les deux lignes tangentes à la parabole qui passent par les extrémités du côté droit forment un angle de 45º avec le côté droit lui-même et se coupent également au sommet de la parabole.

équations de parabole

L’équation d’une parabole est un type de fonction quadratique car elle doit toujours avoir au moins 1 terme au carré. De plus, l’équation d’une parabole dépend de son orientation horizontale ou verticale.

Ainsi, en géométrie analytique, il existe plusieurs manières d’exprimer mathématiquement une parabole : l’ équation canonique ou réduite , l’ équation ordinaire et l’ équation générale de la parabole.

Équation réduite ou canonique de la parabole

Ce qui différencie l’équation réduite ou canonique des autres équations paraboliques est que le sommet de la parabole est l’origine des coordonnées , c’est-à-dire le point (0,0).

La forme de l’équation réduite de la parabole dépend si elle est horizontale ou verticale. Regardez la représentation graphique suivante où les 4 variantes possibles sont indiquées :

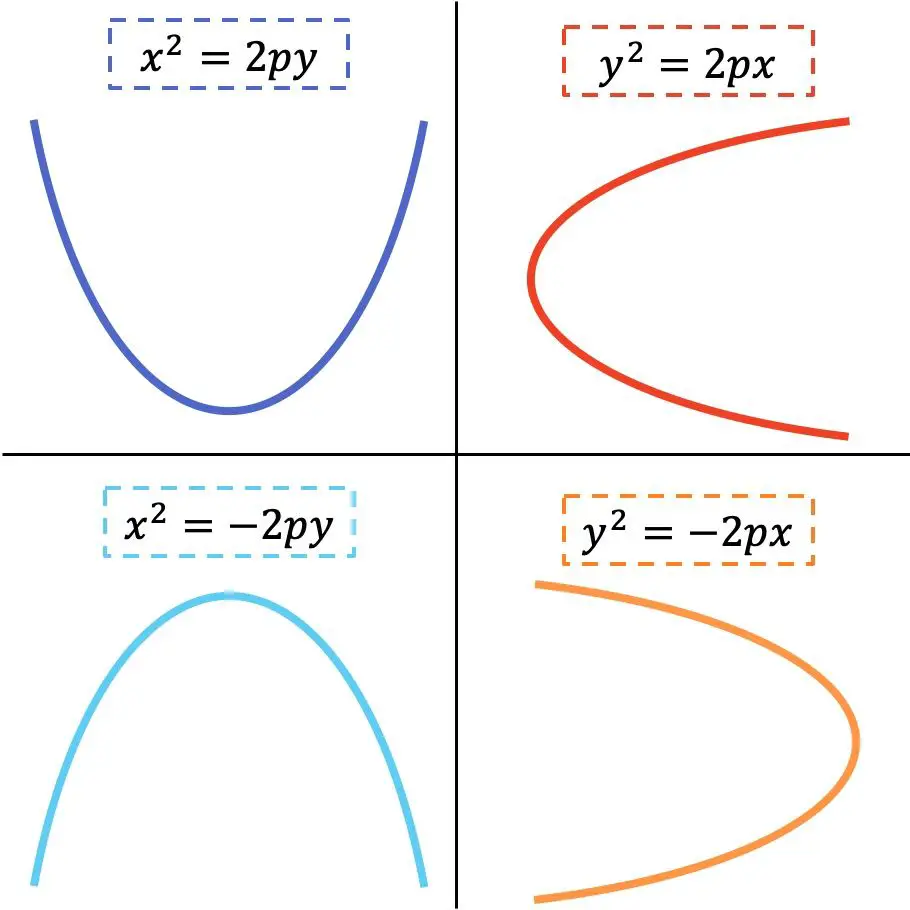
Où

$p$ est le paramètre caractéristique de la parabole.

Comme vous pouvez le voir sur l’image précédente, lorsque la variable x est au carré, la parabole est verticale, en revanche, lorsque la variable y est au carré, la parabole est horizontale. Par contre, le sens des branches de la parabole dépend du signe de l’équation.

Équation ordinaire de la parabole

Nous venons de voir à quoi ressemble l’équation de la parabole lorsque son sommet ou centre correspond à l’origine des coordonnées (l’équation réduite ou canonique), mais quelle est l’équation de la parabole si le sommet est hors de l’origine ?

Lorsque le sommet de la parabole est un point quelconque, on utilise l’équation ordinaire de la parabole , dont l’expression est :

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}$

où le centre ou le sommet de la parabole est le point

$V(x_0,y_0).$

L’équation précédente correspond à la parabole orientée verticalement, c’est-à-dire que l’axe focal de la parabole est parallèle à l’axe Y.

De même, pour définir une parabole orientée horizontalement (son axe focal est parallèle à l’axe X), il faut utiliser la variante suivante de l’équation ordinaire de la parabole :

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}$

Où, comme précédemment, le centre ou sommet de la parabole est le point

$V(x_0,y_0).$

Équation générale de la parabole

Jusqu’ici toutes les équations des paraboles que nous avons analysées servent à exprimer des paraboles horizontales ou verticales. Mais évidemment une parabole peut aussi être oblique ou inclinée .

Eh bien, pour exprimer ce type de paraboles, on utilise l’ équation générale de la parabole , dont la formule est la suivante :

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}$

L’équation ci-dessus est une parabole si et seulement si les coefficients

$A$ et $C$ ne sont pas simultanément nuls et, de plus, la condition suivante est remplie :

$B^2-4AC =0$

Exemple de comment trouver le sommet, le foyer et la directrice d’une parabole à partir de son équation

Dans de nombreux exercices et problèmes de paraboles, on vous demande de calculer le sommet, le foyer et la directrice d’une certaine parabole. Par conséquent, voyons comment cela se fait à travers un exemple :

Trouvez le sommet, le foyer et la directrice de la parabole suivante :

$x^2 = 4y$

La chose fondamentale pour résoudre ce type de problème de parabole est de déterminer le paramètre p de la parabole . Dans ce cas, l’équation de la parabole correspond à l’équation réduite ou canonique (parabole verticale) :

$x^2 = 2py$

Par conséquent, le paramètre p est :

$2p = 4$

$p = \cfrac{4}{2}$

$p = 2$

D’autre part, puisque la parabole suit l’équation réduite ou canonique, cela signifie que son sommet ou centre est à l’origine des coordonnées :

$\bm{V(0,0)}$

Une fois que nous connaissons le sommet et la valeur du paramètre de la parabole, nous pouvons facilement trouver son foyer et sa directrice.

Le terme quadratique de l’équation est la variable x de sorte que l’axe de la parabole sera parallèle à l’axe OY et, en fait, puisque son sommet est le point (0,0), l’axe de la parabole sera l’axe OY lui-même. Alors, le foyer d’une parabole est toujours situé sur l’axe de la parabole et à une distance de

$p/2$ du sommet de la parabole, donc ses coordonnées sont :

$\displaystyle F\left(0, \frac{p}{2} \right)$

$\displaystyle F\left(0, \frac{2}{2} \right)$

$\displaystyle \bm{F\left(0,1 \right)}$

De la même manière, la ligne directrice sera la ligne horizontale qui est à une distance

$p/2$ du sommet de la parabole, qui est l’origine des coordonnées. L’équation de la droite sera donc :

$y=-\cfrac{p}{2}$

$y=-\cfrac{2}{2}$

$\bm{y=-1}}$

La parabole a été représentée graphiquement ci-dessous afin que vous puissiez vérifier les résultats :

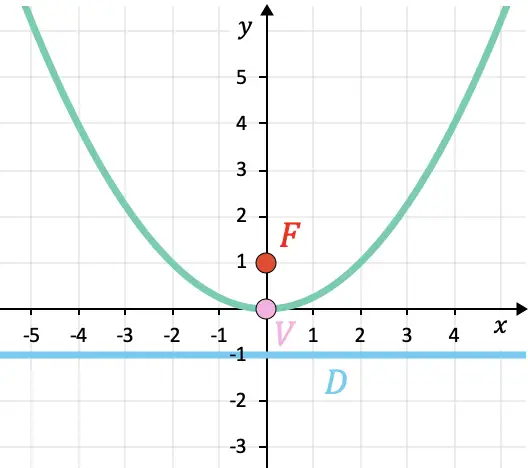
exercices résolus d'équation de la parabole

Propriétés des paraboles

Toutes les paraboles ont les propriétés suivantes :

Une parabole est une courbe ouverte, ou en d’autres termes, elle est constituée de deux branches sans points communs qui s’étendent de façon illimitée.
Chaque parabole a un axe de symétrie unique, où se trouve le sommet de ladite parabole.
Une parabole orientée verticalement est convexe lorsque ses branches montent, au contraire, la parabole est concave si ses branches descendent.
L’excentricité d’une parabole est équivalente à l’unité (1). L’excentricité est un coefficient qui dans ce cas est calculé en divisant la distance du foyer au centre de la parabole par la distance du sommet à la directrice (et les deux distances coïncident toujours dans leur valeur).
De la propriété précédente, il résulte que toutes les paraboles sont similaires ou similaires.
Une parabole n’a pas d’asymptotes.

applications paraboliques

Maintenant que vous connaissez très bien le sens d’une parabole, vous vous demandez peut-être… à quoi sert une parabole ?

Eh bien, même si cela ne vous semble pas, la forme géométrique d’une parabole est très courante dans la vie réelle. Par exemple, plusieurs fois en lançant une balle, elle fait un mouvement parabolique, en particulier au basket. Eh bien, l’équation de la parabole est très utile pour étudier analytiquement la trajectoire parabolique que suit la balle.

Une autre application de la parabole concerne les antennes (d’où le nom d’antenne parabolique). Étant donné que chaque rayon qui tombe sur un objet de forme parabolique parallèle à l’axe de symétrie est réfléchi directement vers le foyer, c’est-à-dire que tous les rayons qui vont à l’antenne parabolique sont concentrés au foyer et cela peut être utilisé de différentes manières. C’est pourquoi le centre d’intérêt d’une parabole est si important.

Problèmes de paraboles résolus

Exercice 1

Calculer le sommet, le foyer et la directrice de la parabole dont l’équation est la suivante :

$y^2 = 8x$

voir solution

Premièrement, la parabole sera horizontale car elle suit l’expression suivante de l’équation réduite ou canonique de la parabole :

$y^2 = 2px$

Donc son paramètre p est :

$2p = 8$

$p = \cfrac{8}{2}$

$p = 4$

D’autre part, puisque la parabole suit l’équation réduite ou canonique, cela signifie que son sommet ou centre est à l’origine des coordonnées :

$\bm{V(0,0)}$

Une fois que nous connaissons le sommet et la valeur du paramètre de la parabole, nous pouvons facilement calculer son foyer et sa directrice.

Le terme quadratique de l’équation est la variable et c’est-à-dire que l’axe de la parabole sera parallèle à l’axe OX et, en fait, puisque son sommet est le point (0,0), l’axe de la parabole sera l’axe OX lui-même. Alors, le foyer d’une parabole est toujours situé sur l’axe de la parabole et à une distance de

$p/2$ du sommet de la parabole, dont les coordonnées sont :

$\displaystyle F\left(\frac{p}{2},0\right)$

$\displaystyle F\left(\frac{4}{2},0\right)$

$\displaystyle \bm{F\left(2,0 \right)}$

De même, la ligne directrice est à une distance

$p/2$ du sommet de la parabole, qui est l’origine des coordonnées et est perpendiculaire à son axe focal. L’équation de la droite directrice est donc :

$x=-\cfrac{p}{2}$

$x=-\cfrac{4}{2}$

$\bm{x=-2}}$

Exercice 2

Trouver le sommet, le foyer et la directrice de la parabole dont l’équation est la suivante :

$(x-4)^2 = -16(y+1)$

voir solution

La parabole est définie selon son équation ordinaire (axe parallèle à l’axe Y), dont la formule est :

$(x-x_0 )^2 = 2p (y-y_0)$

Donc son paramètre p est :

$2p = -16$

$p =- \cfrac{16}{2}$

$p =- 8$

D’autre part, dans ce cas l’équation ordinaire de la parabole implique que son centre n’est pas à l’origine des coordonnées, d’autre part, les coordonnées cartésiennes du sommet de la parabole sont les nombres entre parenthèses avec leur signe changé :

$\bm{V(4,-1)}$

Une fois que nous connaissons le sommet et la valeur du paramètre de la parabole, nous pouvons calculer son foyer et sa directrice.

Le terme quadratique de l’équation est la variable x pour que l’axe de la parabole soit parallèle à l’axe OY. Ainsi, le foyer d’une parabole est toujours situé sur l’axe de la parabole et à une distance de

$p/2$ du sommet de la parabole, de sorte que les coordonnées du foyer soient celles du sommet en ajoutant $p/2$ verticalement:

$\displaystyle F\left(4,-1+\frac{p}{2}\right)$

$\displaystyle F\left(4,-1+\frac{-8}{2}\right)$

$\displaystyle F\left(4,-1-4\right)$

$\displaystyle \bm{F\left(4,-5 \right)}$

De même, la directrice sera la ligne horizontale située à une distance

$p/2$ du sommet de la parabole. L’équation de la droite directrice est donc :

$y=-1-\cfrac{-p}{2}$

$y=-1-\cfrac{-8}{2}$

$y=-1+4$

$\bm{y=3}}$

Exercice 3

Déterminer l’équation parabolique dont l’axe est parallèle à l’axe des abscisses, a pour sommet le point V(5,2) et son foyer est le point P(8,2).

voir solution

Dans ce cas, le sommet de la parabole n’est pas l’origine des coordonnées, nous avons donc besoin de l’équation ordinaire pour définir la parabole de l’énoncé. Aussi, l’axe focal de la parabole est parallèle à l’axe des x, ce qui signifie que la parabole sera orientée horizontalement (les branches iront vers la droite ou vers la gauche) et donc le terme quadratique de l’équation doit être la variable y :

$(y-y_0 )^2 = 2p (x-x_0)$