Vous trouverez ici tout sur l’hyperbole : qu’est-ce que c’est, quels sont ses éléments caractéristiques, comment trouver son équation, des exemples, des exercices résolus,…
Qu’est-ce qu’une hyperbole ?
L’hyperbole est une courbe ouverte à deux branches, dont la définition mathématique est la suivante :
En géométrie analytique, une hyperbole est le lieu des points du plan qui remplissent la condition suivante : la valeur absolue de la différence des distances entre n’importe quel point de l’hyperbole et deux points fixes (appelés foyers) doit être constante.
De plus, la valeur de la soustraction de ces deux distances est toujours équivalente à la distance entre les deux sommets de l’hyperbole.
![]()

Ci-dessous, nous verrons ce que signifie le coefficient
![]() d’une hyperbole.
d’une hyperbole.
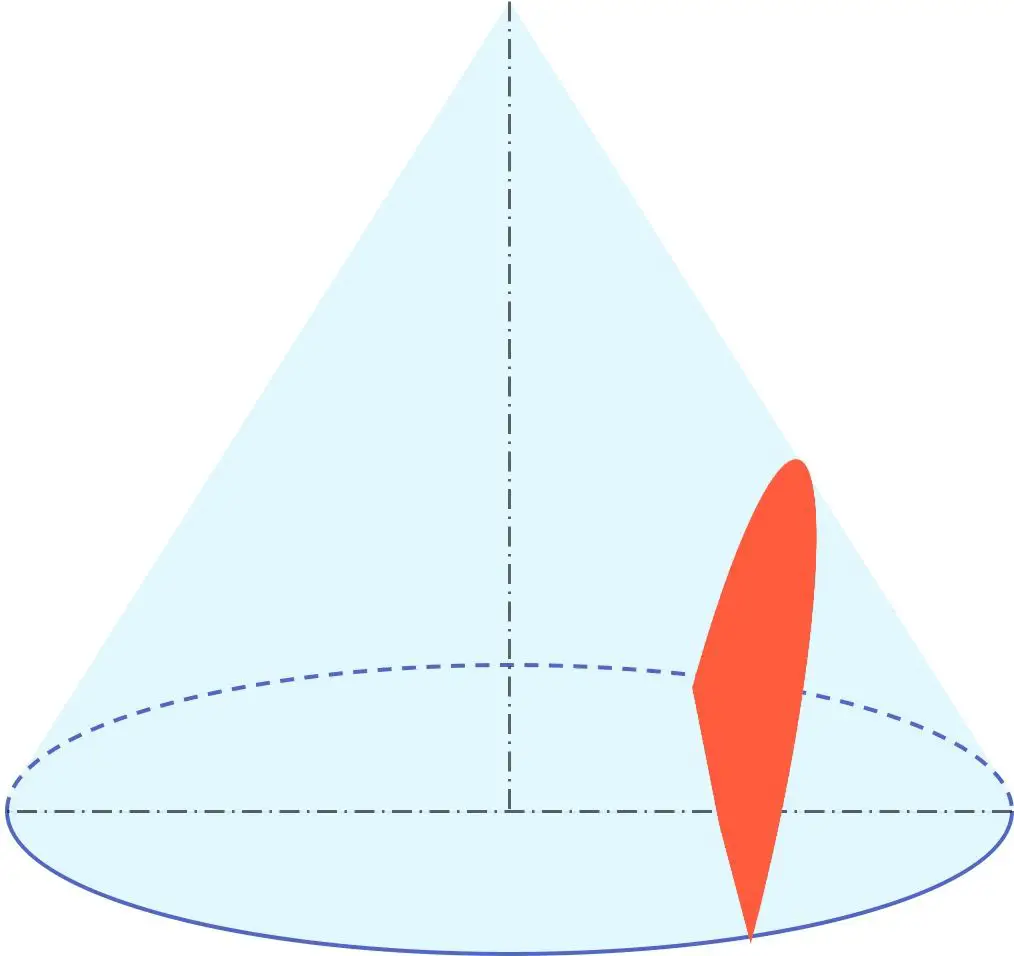
De plus, l’hyperbole fait partie du groupe géométrique appelé coniques avec la circonférence, l’ellipse et la parabole. Par conséquent, une hyperbole est une section conique, ou en d’autres termes, elle peut être obtenue à partir d’un cône.
En particulier, une hyperbole est le résultat de la coupe d’un cône par un plan avec un angle inférieur à l’angle formé par la génératrice du cône par rapport à son axe de révolution.
Éléments d’une hyperbole
Les caractéristiques d’une hyperbole dépendent des éléments suivants :
- Les foyers : ce sont deux points fixes caractéristiques de chaque hyperbole (points F et F’ dans le graphe ci-dessous). La valeur absolue de la différence entre les distances de tout point de l’hyperbole à chaque foyer est constante et égale à

- Axe focal ou principal : c’est la droite qui passe par les deux foyers de l’hyperbole. Il correspond à un axe de symétrie de ladite figure géométrique. Aussi appelé axe transversal ou transversal.
- Axe secondaire : c’est la bissectrice du segment FF’ (droite passant par les points B et B’). De plus, c’est une droite perpendiculaire à l’axe focal et c’est un autre axe de symétrie de l’hyperbole
- Centre (O) : est le point d’intersection des deux axes et le milieu des deux sommets et des deux foyers. Puisque l’hyperbole a deux axes de symétrie, c’est aussi le centre de symétrie.
- Sommets (A et A’) : sont les points d’intersection des branches de l’hyperbole avec l’axe focal.
- Rayons vectoriels (R) : ce sont les segments qui vont de n’importe quel point de l’hyperbole à chaque foyer.
- Distance focale : c’est la longueur du segment composite entre les deux foyers.
- Grand axe ou axe réel : c’est le segment qui va du point A au point A’, sa longueur est équivalente à

- Petit axe ou axe imaginaire : c’est le segment qui va du point B au point B’, sa longueur est équivalente à
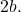
- Asymptotes : sont les lignes pointillées représentées sur le graphique. Nous verrons ci-dessous comment ils sont calculés.
Relation entre les éléments d’une hyperbole
En premier lieu, on dit que le demi-axe signifie la moitié d’un axe. Par exemple, le vrai demi-axe est le segment qui va du point A au centre de l’hyperbole, dont la longueur est
![]()
Ainsi, il existe une relation très importante entre le demi-axe réel, le demi-axe imaginaire et la demi-distance focale. En fait, la formule que nous allons déduire ensuite est beaucoup utilisée pour résoudre des exercices et des problèmes d’hyperboles.
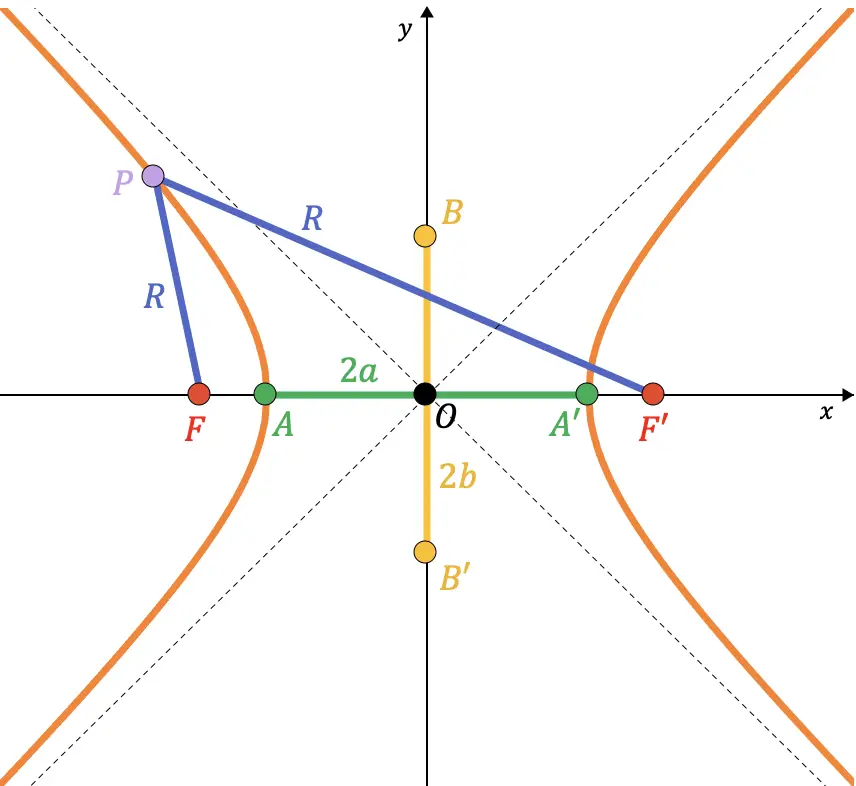
Il faut savoir que les points B et B’ d’une hyperbole correspondent aux points d’intersection de l’axe principal et du cercle imaginaire de rayon
![]() (distance semi-focale) de centre au point A. Par conséquent, comme vous pouvez le voir dans la représentation graphique suivante, le segment qui joint le point A et le point B coïncide avec le rayon dudit cercle (
(distance semi-focale) de centre au point A. Par conséquent, comme vous pouvez le voir dans la représentation graphique suivante, le segment qui joint le point A et le point B coïncide avec le rayon dudit cercle (![]() ):
):
De sorte qu’il peut être démontré à partir du théorème de Pythagore que la relation entre les paramètres
![]() et
et![]() est la suivante:
est la suivante:
![]()
équation d’hyperbole
Il existe plusieurs types d’équations de l’hyperbole, puisque selon ses propriétés l’une ou l’autre sert à l’exprimer mathématiquement. Ensuite, nous analyserons chacun en détail.
Tout d’abord, nous avons l’ équation ordinaire de l’hyperbole. Dans un second temps, nous verrons une variante de l’équation ordinaire, c’est l’ équation réduite ou canonique de l’hyperbole. Ensuite, nous étudierons comment est l’ équation générale d’une hyperbole. Et enfin, nous analyserons les équations de deux cas particuliers d’hyperboles : l’ hyperbole équilatérale et les hyperboles conjuguées .
Équation ordinaire de l’hyperbole
Lorsque l’on veut définir par une équation une hyperbole de centre extérieur à l’origine des coordonnées (point (0,0)), il faut utiliser la formule suivante :
La formule de l’ équation ordinaire de l’hyperbole en coordonnées cartésiennes est la suivante :
![]()
Où:
 et
et sont les coordonnées du centre de l’hyperbole :
sont les coordonnées du centre de l’hyperbole :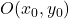
 est la longueur du demi-grand axe de l’hyperbole.
est la longueur du demi-grand axe de l’hyperbole. est la longueur du demi-petit axe de l’hyperbole.
est la longueur du demi-petit axe de l’hyperbole.
Avec cette équation, vous pouvez décrire des hyperboles dont l’axe focal est horizontal (branches ouvertes à gauche et à droite), ce que sont normalement les hyperboles. Mais si on travaille avec un axe focal vertical (branches ouvertes de haut en bas), le signe négatif passe de la variable y à la variable x :
![]()
Où
![]() et
et![]() sont, comme précédemment, les coordonnées du centre de l’hyperbole et les termes
sont, comme précédemment, les coordonnées du centre de l’hyperbole et les termes![]() et
et![]() ils sont toujours le demi-grand axe et le demi-petit axe de l’hyperbole, bien que, contrairement à avant, ces deux seront désormais orientés respectivement verticalement et horizontalement.
ils sont toujours le demi-grand axe et le demi-petit axe de l’hyperbole, bien que, contrairement à avant, ces deux seront désormais orientés respectivement verticalement et horizontalement.
Équation canonique ou réduite de l’hyperbole
Ce type d’équation de l’hyperbole est très similaire à l’équation ordinaire, la seule différence est que l’équation canonique est utilisée pour exprimer analytiquement les hyperboles dont le centre est le point (0,0). Par conséquent, nous utilisons l’équation canonique ou réduite de l’hyperbole lorsque le centre de l’hyperbole est l’origine des coordonnées.
Nous allons maintenant déduire la formule de l’équation réduite de l’hyperbole à partir de son équation ordinaire :
![]()
Si le centre de l’hyperbole doit être l’origine des coordonnées, c’est-à-dire le point (0,0), ce qui suit sera toujours vrai :
![]()
![]()
Ainsi, la formule d’équation canonique ou réduite de l’hyperbole sera :
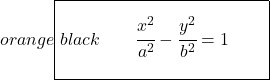
Comme précédemment, si l’axe focal était vertical au lieu d’horizontal, la variable négative serait x :
![]()
Équation générale de l’hyperbole
La formule de l’équation générale d’une hyperbole est la suivante :
![]()
Cependant, pour que l’équation ci-dessus soit une hyperbole, les coefficients
![]() et
et![]() Ils doivent être différents de zéro et, en même temps, avoir le signe opposé.
Ils doivent être différents de zéro et, en même temps, avoir le signe opposé.
Équation d’hyperbole équilatérale
Une hyperbole équilatérale est une hyperbole dans laquelle la longueur du demi-axe réel est équivalente à la longueur du demi-axe imaginaire, cela signifie que
![]() Par conséquent, l’équation d’une hyperbole équilatérale est la suivante :
Par conséquent, l’équation d’une hyperbole équilatérale est la suivante :
![]()
De plus, les asymptotes des hyperboles équilatérales sont perpendiculaires les unes aux autres. Et les équations de ces droites sont les suivantes :
![]()
![]()
Si nous regardons attentivement, ces deux équations sont respectivement les bissectrices du premier (et troisième) quadrant et du deuxième (et quatrième) quadrant. Donc si on fait tourner une hyperbole équilatérale de 45° vers la gauche, ses asymptotes viennent occuper la place des axes de coordonnées :
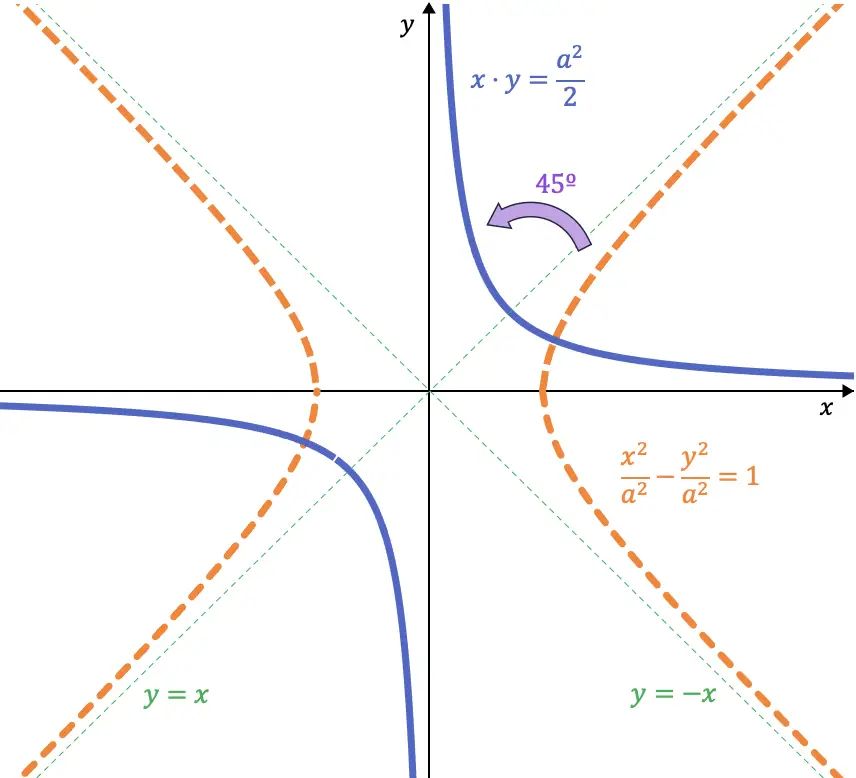
Ainsi, lorsque nous effectuons le virage à 45º, l’équation de l’hyperbole est la suivante :
![]()
hyperboles conjuguées
Deux hyperboles sont conjuguées si l’axe réel de l’une est équivalent à l’axe imaginaire de l’autre . Par conséquent, la seule différence entre les équations de deux hyperboles conjuguées est la variable qui est niée, car les coefficients des dénominateurs doivent rester les mêmes.
Voici un exemple des équations de deux hyperboles conjuguées l’une à l’autre :
![]()
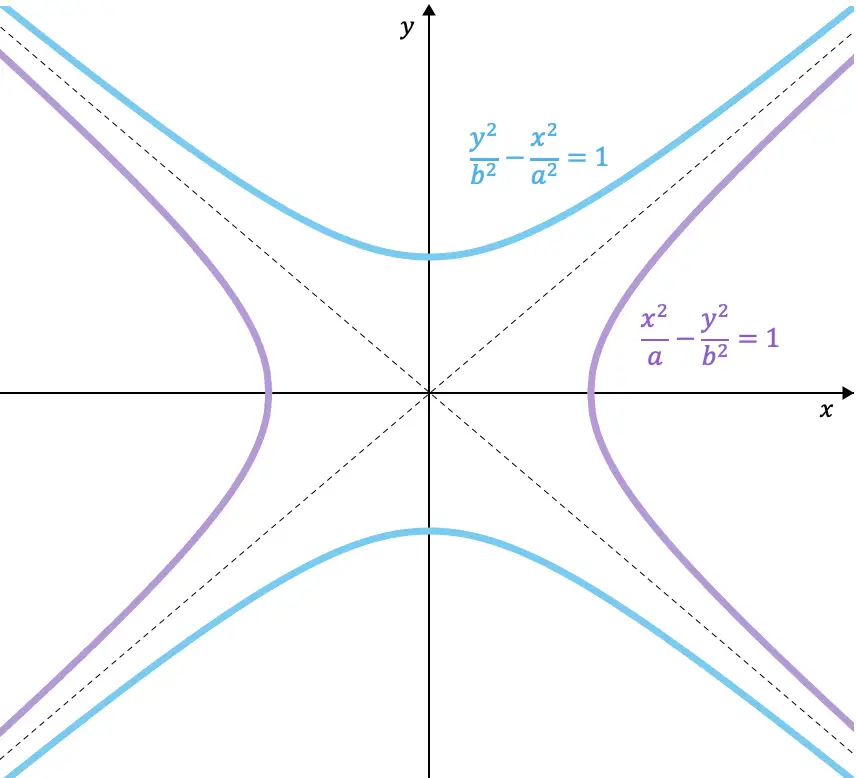
De plus, comme vous pouvez le voir sur les hyperboles qui ont été représentées graphiquement, les hyperboles conjuguées partagent les mêmes asymptotes.
Asymptotes de l’hyperbole
Comme vous l’avez vu dans les graphiques précédents, chaque hyperbole a deux asymptotes. N’oubliez pas qu’une asymptote est une ligne droite qui s’approche très près d’une fonction mais ne la croise jamais tout à fait ou ne la touche pas.
Alors, les formules qui correspondent aux asymptotes des hyperboles sont :
![]()
![]()
Pour que les asymptotes de toute hyperbole puissent être facilement déterminées grâce à leurs coefficients
![]() et
et![]() qui sont respectivement les longueurs du demi-axe réel et du demi-axe imaginaire de l’hyperbole.
qui sont respectivement les longueurs du demi-axe réel et du demi-axe imaginaire de l’hyperbole.
Excentricité de l’hyperbole
L’ excentricité d’une hyperbole est un paramètre caractéristique qui détermine son degré d’ouverture ou de fermeture. Numériquement, l’excentricité d’une hyperbole se calcule en divisant sa demi-focale par son demi-axe réel :
![]()
L’excentricité de toute hyperbole est toujours supérieure à 1 :
![]()
La valeur de ce paramètre est tout à fait pertinente, puisqu’elle indique la forme d’une hyperbole donnée. Plus l’excentricité d’une hyperbole est proche de 1, plus ses branches seront fermées ; en revanche, plus la valeur de l’excentricité est grande, plus ses branches seront ouvertes.
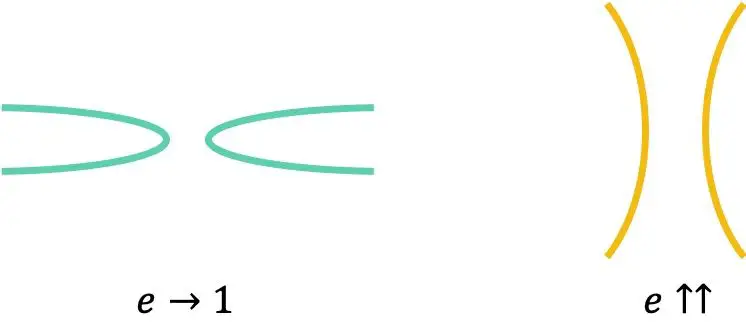
Enfin, il convient de noter que l’excentricité d’une hyperbole équilatérale est toujours égale à
![]()
Problèmes d’hyperboles résolus
Ci-dessous, vous pouvez pratiquer les concepts que nous avons vus avec des problèmes et des exercices résolus d’hyperboles et l’équation de l’hyperbole.
Exercice 1
Quelle est l’équation de l’hyperbole de centre au point (-1,3), de longueur du demi-axe réel de 3 unités et de longueur du demi-axe imaginaire (parallèle à l’axe Y) de 7 unités ?
Pour trouver l’équation de l’hyperbole il suffit d’appliquer la formule de l’équation ordinaire de l’hyperbole :
![]()
Nous substituons les coordonnées du centre de l’hyperbole dans l’équation :
![]()
![]()
Et enfin, on substitue les valeurs des inconnues
![]() et
et ![]()
![]()
![]()
Exercice 2
Trouver les coordonnées du centre, des sommets, des foyers, la valeur de l’excentricité et les asymptotes de l’hyperbole dont l’équation est définie par :
![]()
Tout d’abord, il faut noter que la variable négative de l’équation est la variable y , donc les branches de l’hyperbole s’ouvriront à droite et à gauche (axe focal parallèle à l’axe X).
Deuxièmement, l’équation correspond à l’équation canonique (ou réduite) de l’hyperbole, donc son centre est l’origine des coordonnées.
![]()
Une fois que nous connaissons le centre de l’hyperbole, pour calculer tout le reste, nous devons trouver la valeur du demi-axe réel (paramètre
![]() ) et le demi-axe imaginaire (paramètre
) et le demi-axe imaginaire (paramètre![]() ). On peut déduire les deux de la formule de l’équation canonique (ou réduite) de l’hyperbole :
). On peut déduire les deux de la formule de l’équation canonique (ou réduite) de l’hyperbole :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Donc s’il y a une distance de 5 unités entre le centre et les sommets, cela implique que les sommets des hyperboles sont :
![]()
Pour déterminer les coordonnées de chaque foyer, il faut connaître la valeur de la demi-distance focale (paramètre
![]() ). Et, pour cela, on peut utiliser la formule qui relie les éléments d’une hyperbole :
). Et, pour cela, on peut utiliser la formule qui relie les éléments d’une hyperbole :
![]()
![]()
![]()
Il y a donc un espace de 13 unités entre le centre et les foyers. Ainsi, les coordonnées de chaque foyer sont :
![]()
Ensuite, pour calculer l’excentricité de l’hyperbole, nous devons utiliser sa formule correspondante :
![]()
Et, enfin, on trouve les asymptotes de l’hyperbole avec leurs formules :
![]()
![]()
Exercice 3
Calculer l’équation de l’hyperbole de centre à l’origine des coordonnées sachant que la différence des distances d’un point de l’hyperbole aux foyers F(-4,0) et F(4,0) est de 6 unités.
Tout d’abord, puisque l’hyperbole a le centre à l’origine des coordonnées, nous utiliserons l’équation canonique ou réduite :
![]()
Ensuite, selon la définition d’une hyperbole, la valeur absolue de la différence des distances de l’un de ses points aux foyers (qui dans ce cas est 6) doit être égale à la longueur de l’axe réel (
![]() ). Pourtant:
). Pourtant:
![]()
![]()
![]()
![]()
D’autre part, le centre de l’hyperbole est le point (0,0) et un foyer est le point (4,0). Pour que la distance aux deux points (paramètre
![]() ) sont 4 unités.
) sont 4 unités.
![]()
Nous pouvons maintenant connaître la valeur du paramètre
![]() avec la relation mathématique entre les 3 coefficients caractéristiques de l’hyperbole :
avec la relation mathématique entre les 3 coefficients caractéristiques de l’hyperbole :
![]()
![]()
![]()
![]()
Donc l’équation de l’hyperbole est :
![]()
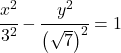
![]()