Cette page explique les différentes positions relatives qui existent entre une ligne et un cercle. De plus, vous pourrez voir comment trouver la position relative entre une ligne et un cercle.
Quelles sont les positions relatives d’une droite et d’un cercle ?
En géométrie analytique, la position relative d’une droite par rapport à un cercle ne peut être qu’extérieure, tangente ou sécante :
- Extérieur : lorsque la distance entre la ligne et le centre du cercle est supérieure au rayon.
- Tangente : lorsque la distance entre la droite et le centre du cercle est égale au rayon.
- Sécante : lorsque la distance entre la droite et le centre du cercle est inférieure au rayon.
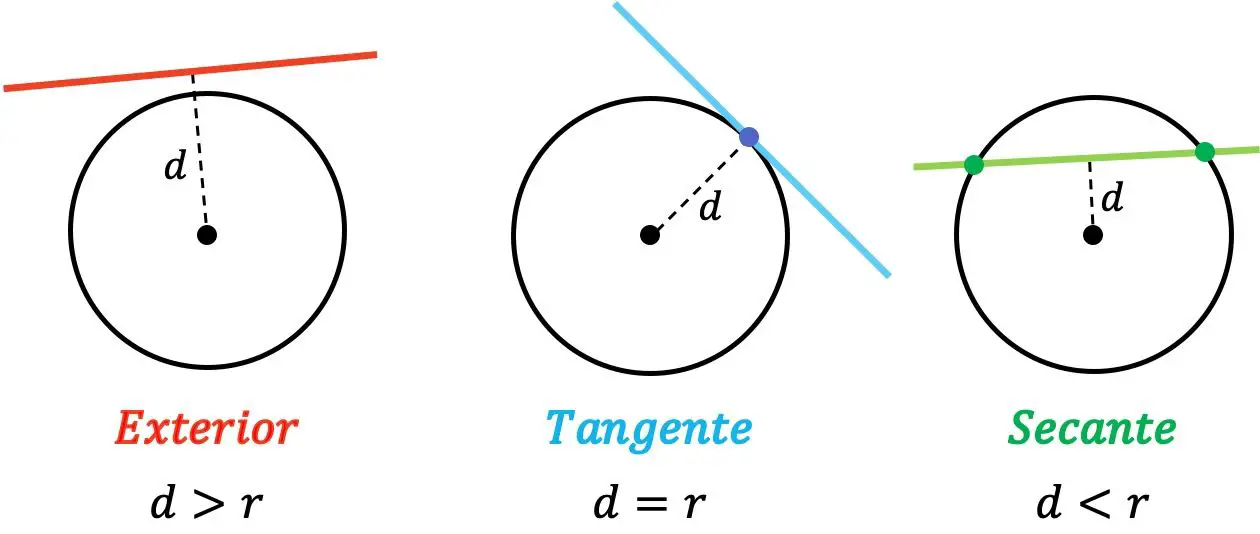
Donc, si une droite est extérieure à un cercle, elle ne le coupe en aucun point. En revanche, lorsque la droite est tangente au cercle, les deux ont un point commun. Et enfin, une droite est sécante à un cercle lorsqu’elle le coupe en deux points différents.
Comment déterminer la position relative entre une droite et un cercle ?
Il existe deux manières de connaître la position relative d’une droite par rapport à un cercle dans le plan : l’une en calculant la distance entre la droite et le centre du cercle, et l’autre en résolvant un système d’équations composé de l’équation de la droite et de l’équation du cercle.
Ensuite, nous verrons exactement en quoi consiste chaque méthode.
Méthode 1 : Distance entre la ligne et le centre du cercle
Comme nous l’avons vu dans l’explication du concept de position relative entre une ligne et un cercle, la distance entre une ligne et le centre d’un cercle indique de quel type de position relative il s’agit.
Cette méthode consiste donc à trouver la distance entre la droite et le centre du cercle. Évidemment, pour pouvoir le faire, vous devez savoir calculer la distance entre un point et une ligne , sur cette page vous pouvez voir comment le faire, ainsi que des exemples et des exercices résolus à pratiquer.
Ainsi, selon le résultat de la distance obtenue, ce sera un cas ou un autre :
- La ligne sera à l’extérieur du cercle si la distance obtenue est supérieure au rayon du cercle.
- La droite sera tangente au cercle si la distance obtenue est équivalente au rayon du cercle.
- La droite sera sécante au cercle si la distance obtenue est inférieure au rayon du cercle.
Méthode 2 : résoudre un système d’équations
Une autre façon de connaître la position relative d’une ligne par rapport à un cercle consiste à utiliser un système d’équations formé par l’équation de la ligne et l’équation du cercle. Évidemment, pour appliquer cette méthode, vous devez savoir quelle est l’équation de la circonférence et quelle est la formule de l’équation de la ligne .
Selon le nombre de solutions du système d’équations, nous serons devant un cas ou un autre :
- Si le système d’équations n’a pas de solution, cela signifie que la droite et le cercle n’ont pas de point commun, donc la droite est à l’extérieur du cercle.
- Si le système d’équations a 1 solution, cela implique que la droite et le cercle ont un point commun, donc la droite est tangente au cercle.
- Si le système d’équations a 2 solutions, cela signifie que la droite et le cercle ont deux points en commun, de sorte que la droite est sécante au cercle.