Vous trouverez ici comment calculer le point de symétrie par rapport à un autre point, par rapport à une droite et par rapport à un plan. De plus, vous pourrez voir des exemples et des exercices résolus étape par étape.
Point symétrique par rapport à un autre point
Avant de regarder comment le point symétrique est calculé, passons en revue ce qu’est exactement un point symétrique par rapport à un autre point :
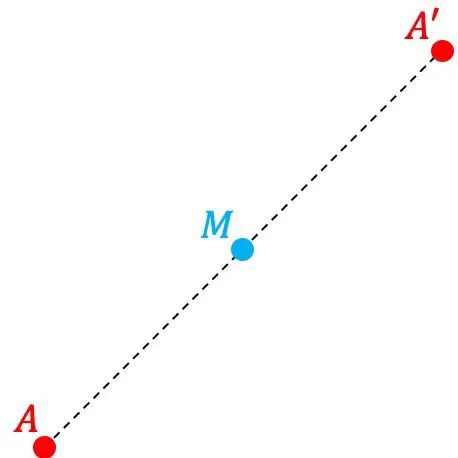
Le point A’ est le point symétrique du point A par rapport à un autre point M si le point A’ est situé symétriquement à la même distance du point M que la distance entre les points A et M. Par conséquent, M est le milieu du segment formé par les points A et A’.
![]()
D’autre part, on dit aussi que le point M est le centre de symétrie.
Ainsi, pour calculer les coordonnées du point de symétrie, nous allons utiliser la formule du milieu d’un segment :
![]()
A partir de cette équation on dégage le point inconnu A’ et on obtient la formule du point symétrique par rapport à un autre point :
![]()
Exemple de recherche du point symétrique par rapport à un autre point
A titre d’exemple, nous allons calculer le point de symétrie du point A par rapport au point M. Soit les deux points :
![]()
Pour déterminer le point de symétrie entre ces deux points, on applique la formule du point de symétrie par rapport à un autre :
![]()
Maintenant, nous remplaçons les points dans la formule :
![]()
Et nous opérons :
![]()
![]()
point symétrique par rapport à une droite
Nous venons de voir la notion de point symétrique par rapport à un autre point. Eh bien, le point symétrique d’un point par rapport à une droite est très similaire :
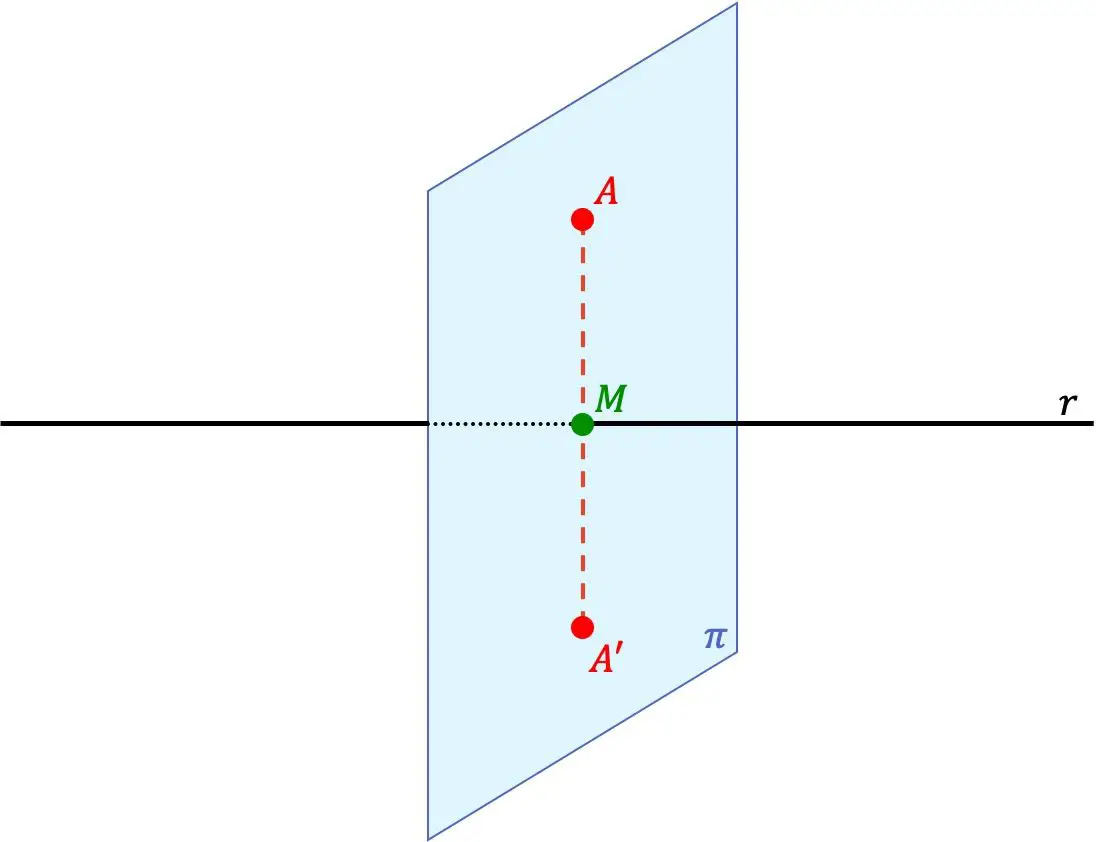
Le point A’ est le point symétrique du point A par rapport à une ligne si les deux points A’ et A se trouvent sur la même ligne perpendiculaire à la ligne et, de plus, la distance entre le point A’ et la ligne est égale à la distance entre le point A et la ligne.
![]()
Donc la droite r est aussi un axe de symétrie entre les points.
Ainsi, pour déterminer le point de symétrie du point A par rapport à la droite r , il faut suivre la procédure suivante :
- On retrouve le plan perpendiculaire à la droite r qui passe par le point A (plan π de la représentation graphique précédente). Pour cela il faut utiliser le vecteur directeur de la droite, qui sera le vecteur normal du plan.
- Nous calculons le point d’intersection entre le plan trouvé et la droite (point M de l’image précédente).
- Nous utilisons la formule du point symétrique par rapport à un point (vue dans la section ci-dessus) pour trouver le point symétrique du point A par rapport au point M. Le résultat est le point symétrique que nous recherchions.
Exemple de calcul du point de symétrie par rapport à une droite
Une fois que l’on sait calculer le point de symétrie d’un autre point par rapport à une droite, on va voir un exercice résolu en exemple :
- Trouver le point symétrique du point A par rapport à la droite r. Etant dit point et ligne :
![Rendered by QuickLaTeX.com \displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5906f8f5fce95109f9f19d93d1f41cd_l3.png)
Premièrement, nous devons calculer le plan perpendiculaire à la droite r qui passe par le point A. Le vecteur normal à ce plan sera le vecteur directeur de la droite, dont les composantes sont les termes devant le paramètre
![]() car elle s’exprime sous forme d’équations paramétriques :
car elle s’exprime sous forme d’équations paramétriques :
![]()
Et les coefficients A, B et C de l’équation d’un plan coïncident avec les coordonnées de son vecteur normal, donc :
![]()
Le point A doit se trouver sur ce plan, nous pouvons donc maintenant substituer le point A dans l’équation du plan pour trouver le coefficient D :
![]()
![]()
![]()
![]()
![]()
De sorte que l’équation du plan perpendiculaire à la droite ry passant par le point A est :
![]()
Une fois que nous connaissons l’équation du plan, nous devons calculer le point d’intersection du plan et de la droite. Pour ce faire, nous substituons les coordonnées de la ligne dans l’équation du plan et résolvons l’équation résultante :
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd611c8a6c7e516dbb67583b49f0b8e6_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
Maintenant, nous remplaçons la valeur de
![]() obtenu dans l’équation de la droite :
obtenu dans l’équation de la droite :
![Rendered by QuickLaTeX.com \displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b0c515e3969169679e810db65a99e3f_l3.png)
Donc le point d’intersection entre la droite r et le plan qui lui est perpendiculaire est :
![]()
Enfin, il suffit de trouver le point symétrique du point A par rapport au point M, pour cela, on peut utiliser la formule vue au début de cette page :
![Rendered by QuickLaTeX.com \begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4b39555d71f045dd42e9422dd077679_l3.png)
point symétrique par rapport à un plan
Avant de voir la méthode pour déterminer le point de symétrie d’un autre point par rapport à un plan, voyons quelle est sa définition :
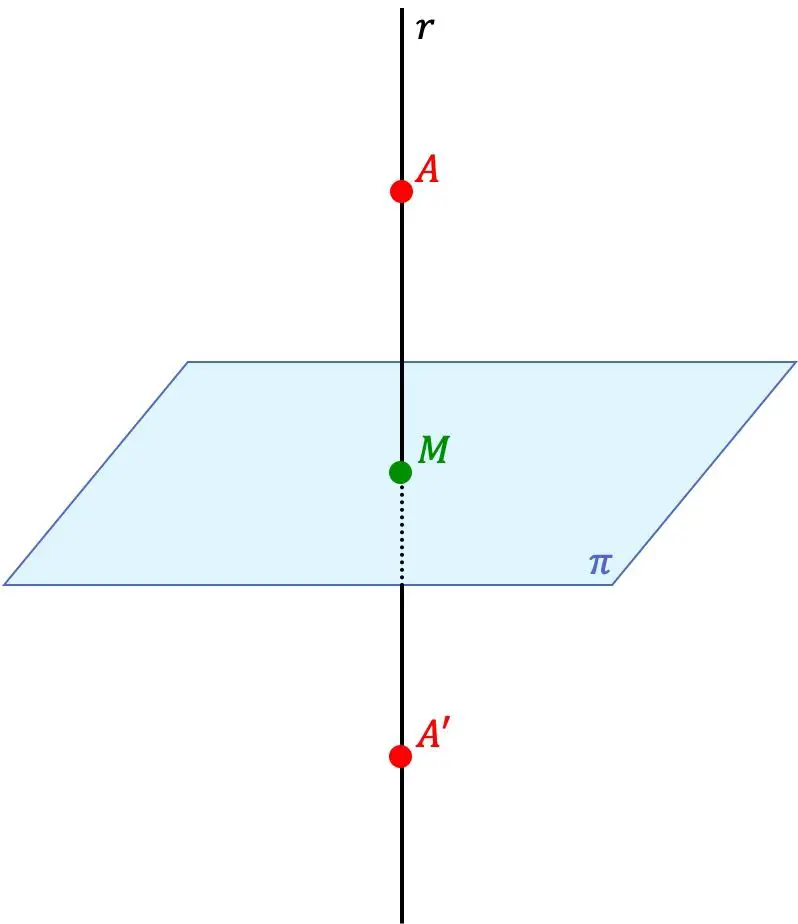
Le point A’ est le point symétrique du point A par rapport à un plan si les deux points A’ et A se trouvent sur la même ligne perpendiculaire au plan et, de plus, la distance entre le point A’ et le plan est équivalente à la distance entre le point A et le plan.
![]()
Donc le plan est aussi un plan de symétrie entre les deux points.
Ainsi, pour connaître les coordonnées cartésiennes du point symétrique du point A par rapport au plan π, il faut suivre les étapes suivantes :
- On trouve l’équation de la droite perpendiculaire au plan qui passe par le point A. Pour cela on va utiliser le vecteur normal au plan comme vecteur directeur de la droite.
- On calcule le point d’intersection entre le plan et la droite trouvée (point M de l’image précédente).
- Nous utilisons la formule du point symétrique par rapport à un point (vu dans la section de début) pour trouver le point symétrique du point A par rapport au point M. Le résultat est le point symétrique que nous recherchions.
Exemple de détermination du point de symétrie par rapport à un plan
Ci-dessous, vous pouvez voir un problème résolu concernant le point de symétrie d’un autre point par rapport à un plan :
- Déterminer le point de symétrie de A par rapport au plan π. Etant dit point et plan :
![]()
La première chose que nous devons faire est de trouver l’équation de la droite perpendiculaire au plan et qui passe par le point A. Pour cela, nous pouvons utiliser le vecteur normal au plan comme vecteur directeur de la droite, dont les composantes X, Y, Z sont les coefficients des termes A, B et C respectivement de l’équation du plan :
![]()
On peut maintenant construire les équations paramétriques de la droite orthogonale au plan avec le vecteur directeur trouvé et un de ses points (point A) :
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ec51a68802f626dcd5cf7a3bc1dda59_l3.png)
Une fois que nous connaissons la droite perpendiculaire, nous calculons le point d’intersection du plan et de la droite en substituant les coordonnées de la droite dans l’équation du plan :
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases} \qquad \qquad \pi : \ 2x+y-z-6=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb4ee2c7f6742eec2e1fa11cac3c5635_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
Maintenant, nous remplaçons la valeur de
![]() obtenu dans l’équation de la droite :
obtenu dans l’équation de la droite :
![Rendered by QuickLaTeX.com \displaystyle t=1 \ \longrightarrow \ \begin{cases}x=3 + 2\cdot 1 =5\\[1.7ex] y=-4 +1=-3\\[1.7ex] z=2-1=1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a9373141f2f699971d5789e1cb0ed0d_l3.png)
Donc le point d’intersection entre le plan et la droite perpendiculaire est :
![]()
Enfin, il suffit de trouver le point symétrique du point A par rapport au point M. Et, pour cela, on peut utiliser la formule vue au début de cette page :
![Rendered by QuickLaTeX.com \begin{aligned} A' & = 2M - A \\[2ex] &= 2(5,-3,1) - (3,-4,2) \\[2ex] & = (10,-6,2)-(3,-4,2)\\[2ex] & = \bm{(7,-2,0)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e8199cf83bc3bdfbf0a7b2adb65a97af_l3.png)