Distance d'un point à un plan dans l'espace (formule)

Sur cette page, vous trouverez comment la distance entre un point et un plan dans l’espace est calculée (formule). De plus, vous pourrez voir des exemples et vous entraîner avec des exercices résolus étape par étape.

Quelle est la distance d’un point à un plan ?

En géométrie analytique, la distance d’un point à un plan est la distance la plus courte entre le point et tout autre point du plan. Cette distance correspond à la longueur du segment perpendiculaire au plan qui va du point au plan.

Formule pour la distance d’un point à un plan

Une fois que nous avons vu exactement la notion de distance entre un point et un plan, voyons maintenant la formule pour calculer ladite distance :

Étant donné un point et l’équation générale (ou implicite) d’un plan :

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

La formule de la distance d’un point à un plan est :

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

La preuve de la formule de la distance d’un point à un plan est assez fastidieuse et longue, nous ne la ferons donc pas sur cette page.

D’autre part, si lors de l’application de la formule nous obtenons un résultat égal à zéro, cela signifie évidemment que la distance entre le point et le plan est nulle et, par conséquent, le point fait partie de ce plan.

Enfin, notez que pour appliquer la formule, le plan doit être défini sous la forme d’une équation générale (ou implicite). Donc si elle était exprimée par un autre type d’équation du plan, il faudrait d’abord la transformer en une équation générale et ensuite utiliser la formule.

Exemple de calcul de la distance d’un point à un plan

Pour que vous puissiez voir comment la distance entre un point et un plan est déterminée numériquement, nous allons résoudre un exemple ci-dessous :

Calculer la distance entre le point P et le plan π. Etant dit point et plan :

$P(1,3,-2) \qquad \qquad \pi: \ 2x+5y-4z+7=0$

Pour trouver la distance du point au plan, il suffit d’appliquer la formule vue dans la section ci-dessus :

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Maintenant, nous substituons la valeur de chaque inconnue dans la formule :

$d(P,\pi) = \cfrac{\lvert 2\cdot 1+5\cdot 3-4\cdot (-2)+7\rvert}{\sqrt{2^2+5^2+(-4)^2}}$

Et, enfin, on fait les opérations :

$d(P,\pi) = \cfrac{\lvert 2+15+8+7\rvert}{\sqrt{4+25+16}}$

$\bm{d(P,\pi) = }\cfrac{\bm{32}}{\bm{\sqrt{45}}}$

Notez que dans le numérateur de la fraction il y a une valeur absolue et dans le dénominateur nous avons une racine carrée, donc le résultat doit toujours être positif. C’est logique car les distances ne peuvent pas être négatives, mais sont toujours positives.

Calculer la distance entre deux plans parallèles

Deux plans parallèles sont toujours à la même distance, par conséquent , pour trouver la distance entre deux plans parallèles, nous pouvons prendre un point sur l’un des deux plans et calculer la distance de ce point à l’autre plan.

C’est une méthode pour trouver la distance entre deux plans parallèles. Cependant, il existe un moyen encore plus simple de le faire lorsque les coefficients A, B et C des équations des deux plans coïncident :

Soit les équations générales (ou implicites) de deux plans parallèles :

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

La formule pour calculer la distance entre deux plans parallèles est :

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

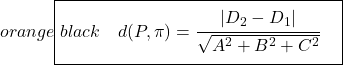
Alors surement il est plus facile de trouver la distance entre deux plans parallèles en utilisant la formule puisqu’il ne s’agit que d’appliquer la formule et c’est tout, mais cela dépend du problème. De plus, nous pensons qu’il est préférable d’expliquer les deux façons de calculer la distance afin que vous puissiez choisir celle que vous préférez.

Exemple de calcul de la distance entre deux plans parallèles

A titre d’exemple, nous allons calculer la distance entre les deux plans suivants :

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Il faut d’abord vérifier qu’on a bien affaire à deux plans parallèles. Ainsi, tous les coefficients des équations des plans sont proportionnels sauf les termes indépendants, ce sont donc effectivement deux plans parallèles.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Dans ce cas, les termes A, B et C des équations des deux plans ne coïncident pas, mais on peut y parvenir en divisant par deux l’équation entière du second plan :

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Ainsi, les équations des deux plans ont déjà les mêmes coefficients A, B et C. Par conséquent, nous pouvons facilement calculer la distance entre les deux plans avec la formule de la distance entre deux plans parallèles :

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Nous substituons les valeurs et résolvons les opérations:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

De sorte que la distance entre un plan et l’autre plan est égale à l’unité.

Résolution des problèmes de distance d’un point à un plan

Exercice 1

Calculer la distance entre le point P et le plan dont l’équation cartésienne (ou générale) est :

$P(2,0,-1) \qquad \qquad \pi: \ x-3y+2z-4=0$

voir solution

Pour calculer la distance du point au plan, il faut utiliser la formule correspondante :

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Nous substituons la valeur de chaque paramètre dans la formule :

$d(P,\pi) = \cfrac{\lvert 1\cdot 2+(-3)\cdot 0+2\cdot (-1)-4\rvert}{\sqrt{1^2+(-3)^2+2^2}}$

Et, enfin, on fait les opérations :

$d(P,\pi) = \cfrac{\lvert 2+0-2-4\rvert}{\sqrt{1+9+4}}$

$d(P,\pi) = \cfrac{\lvert -4\rvert}{\sqrt{14}}$

$\bm{d(P,\pi) = }\cfrac{\bm{4}}{\bm{\sqrt{14}}}$

Exercice 2

Trouver la distance entre le point P et le plan π :

$P(-1,4,3) \qquad \qquad \pi: \ y=5x-2z$

voir solution

Avant d’utiliser la formule de la distance d’un point à un plan, il faut d’abord exprimer le plan sous la forme d’une équation implicite (ou générale) :

$\pi: \ -5x+y+2z=0$

Et maintenant, nous pouvons utiliser la formule pour déterminer la distance du point au plan :

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

On substitue la valeur de chaque terme dans la formule :

$d(P,\pi) = \cfrac{\lvert -5\cdot (-1)+1\cdot 4+2\cdot 3+0\rvert}{\sqrt{(-5)^2+1^2+2^2}}$

Et, pour finir, on fait les opérations :

$d(P,\pi) = \cfrac{\lvert 5+4+6\rvert}{\sqrt{25+1+4}}$

$\bm{d(P,\pi) = }\cfrac{\bm{15}}{\bm{\sqrt{30}}}$

Exercice 3

Utilisez la formule de la distance entre un point et un plan pour déterminer si le point P se trouve dans le plan π.

$P(0,-3,5) \qquad \qquad \pi: \ 4x+6y+2z+8=0$

voir solution

Pour vérifier si le point appartient au plan, on peut calculer la distance entre les deux : si la distance est nulle cela implique que le point appartient bien au plan, par contre si la distance est différente de 0 cela signifie que le point est hors du plan.

Par conséquent, nous déterminons la distance entre le point et le plan à partir de la formule :

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi) = \cfrac{\lvert 4\cdot 0+6\cdot (-3)+2\cdot 5+8\rvert}{\sqrt{4^2+6^2+2^2}}$

$d(P,\pi) = \cfrac{\lvert -18+10+8\rvert}{\sqrt{16+36+4}}$

$d(P,\pi) = \cfrac{0}{\sqrt{56}}$

$\bm{d(P,\pi) = 0}$

La distance entre le point et le plan est équivalente à zéro, donc effectivement le point appartient au plan.

Exercice 4

Trouvez la distance entre les deux plans suivants :

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

voir solution

Il faut d’abord vérifier qu’on a bien affaire à deux plans parallèles. Tous les coefficients des équations des deux plans sont proportionnels à l’exception des termes indépendants, il s’agit donc bien de deux plans parallèles.

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Dans ce cas, nous calculerons la distance entre les deux plans avec la formule, puisque leurs coefficients A, B et C sont égaux :

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Donc, nous substituons les valeurs dans la formule et effectuons les opérations :

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

Exercice 5

Trouver la distance entre les deux plans parallèles suivants :

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

voir solution

Le plan de premier plan est défini sous la forme d’équations paramétriques, donc pour appliquer la formule de la distance entre deux plans parallèles, nous devons d’abord la convertir sous la forme d’une équation générale et cela prend beaucoup de calculs et de temps. Par conséquent, il est plus rapide si nous prenons un point sur ce plan et calculons la distance de ce point à l’autre plan.

Ainsi, les coordonnées d’un point par lequel passe le plan π ₁ correspondent aux termes indépendants de chaque équation paramétrique :

$P(3,-2,5)$