Calculer le point d'intersection ou d'intersection entre deux lignes

Vous trouverez ici comment le point de coupure (ou intersection) entre deux lignes est calculé. Vous verrez également des exemples et vous pourrez vous entraîner avec des exercices résolus étape par étape.

Quel est le point de coupure ou d’intersection entre deux lignes ?

Le point d’intersection (ou coupe) entre deux lignes est le point où deux lignes différentes se croisent. Par conséquent, lorsque deux lignes différentes ont une intersection ou un point de coupe, cela signifie qu’elles coïncident en un point.

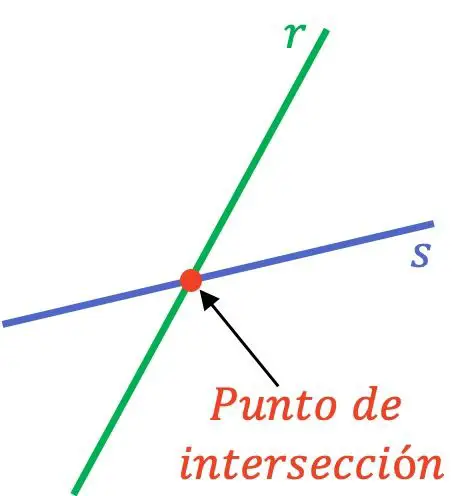
Pour que deux droites se coupent en un point, elles doivent être des droites sécantes, puisque les droites parallèles ne se touchent en aucun point.

Si vous ne vous souvenez plus exactement de ce que sont les lignes qui se croisent maintenant, nous vous recommandons de consulter notre page d’exemples de lignes sécantes , où vous trouverez une explication détaillée de ce que sont ces types de lignes et comment savoir si deux lignes se croisent ou non.

Comment calculer le point de coupure ou d’intersection entre deux lignes ?

Une fois que nous avons vu la définition du point d’intersection ou d’intersection entre deux lignes, voyons maintenant comment ledit point est calculé.

Pour trouver le point d’intersection (ou intersection) entre deux droites, il faut d’abord s’assurer que les deux droites ne sont pas parallèles, car si ce sont deux droites parallèles elles ne se couperont en aucun point. Par conséquent, vous devez d’abord savoir comment déterminer quand deux droites sont parallèles et quand elles ne le sont pas ; Si vous ne vous rappelez pas comment faire, vous pouvez le revoir en cliquant sur le lien.

Une fois que l’on sait que les deux droites ne sont pas parallèles, pour déterminer le point d’intersection (ou intersection) entre les deux droites, il faut résoudre le système d’équations formé par l’équation de chaque droite. Et le résultat dudit système d’équations sera les coordonnées du point d’intersection (ou intersection) entre les deux lignes.

Exemple de comment trouver le point d’intersection ou d’intersection entre deux lignes

A titre d’exemple, nous allons résoudre un problème afin que vous puissiez voir comment trouver le point d’intersection (ou intersection) entre 2 droites :

Trouvez le point d’intersection entre les deux lignes suivantes :

$r: \ y=4x-1 \qquad \qquad s: \ y=-2x+5$

Premièrement, les lignes ne sont pas parallèles car elles ont des pentes différentes, elles se coupent donc toutes les deux en un point du plan cartésien.

Pour le savoir, il faut résoudre le système d’équations composé de l’équation de chaque droite :

$\left. \begin{array}{l} y=4x-1 \\[2ex] y=-2x+5 \end{array} \right\}$

Dans ce cas particulier, on résoudra le système par la méthode d’égalisation puisque les deux inconnues

$y$ sont déjà résolus (les deux lignes sont sous forme d’équation explicite):

$y= y$

$4x-1=-2x+5$

On efface la valeur de la variable

$x:$

$4x+2x=5+1$

$6x=6$

$x = \cfrac{6}{6}$

$x = 1$

Et une fois qu’on sait combien ça vaut

$x,$ Nous substituons sa valeur dans n’importe quelle équation pour trouver la valeur de $y:$

$y=4x-1 \ \xrightarrow{x \ = \ 1} \ y=4\cdot 1-1$

$y =4-1$

$y =3$

De sorte que les coordonnées du point d’intersection entre les deux lignes sont :

$\bm{(1,3)}$

Problèmes résolus du point d’intersection ou d’intersection entre deux lignes

Exercice 1

Quel est le point d’intersection ou d’intersection entre les deux lignes suivantes ?

$r: \ y=x+5 \qquad \qquad s: \ y=2x+3$

voir solution

Premièrement, les droites ne sont pas parallèles car elles ont des pentes différentes, donc les deux droites se rencontreront à un certain point du plan.

Pour calculer ledit point, il faut résoudre le système d’équations formé par l’équation de chaque droite :

$\left. \begin{array}{l} y=x+5 \\[2ex] y=2x+3 \end{array} \right\}$

Dans ce cas, on résoudra le système d’équations par la méthode d’égalisation puisque les deux inconnues

$y$ sont déjà résolus (les deux lignes sont sous forme d’équation explicite):

$y= y$

$x+5=2x+3$

On efface la valeur de la variable

$x:$

$x-2x=3-5$

$-x=-2$

$x=2$

Et une fois qu’on sait combien ça vaut

$x,$ Nous substituons sa valeur dans n’importe quelle équation pour trouver la valeur de $y:$

$y=x+5 \ \xrightarrow{x \ = \ 2} \ y=2+5$

$y =7$

Les coordonnées du point d’intersection entre les deux droites sont donc :

$\bm{(2,7)}$

Exercice 2

Trouvez le point d’intersection ou d’intersection entre les deux lignes suivantes :

$r: \ y=-3x+1 \qquad \qquad s: \ 4x+2y+6=0$

voir solution

le droit

$s$ Elle s’exprime sous la forme d’une équation implicite (ou générale), nous allons donc d’abord la passer sous la forme d’une équation explicite pour connaître la valeur de sa pente :

$4x+2y+6=0$

$2y=-4x-6$

$y=\cfrac{-4x-6}{2}$

$y=-2x-3$

De sorte que les deux lignes ont des pentes différentes et qu’il existe donc un point d’intersection entre elles.

Pour calculer ledit point, il faut résoudre le système d’équations formé par l’équation de chaque droite :

$\left. \begin{array}{l} y=-3x+1\\[2ex] y=-2x-3 \end{array} \right\}$

On résout le système d’équations par la méthode d’égalisation :

$y= y$

$-3x+1=-2x-3$

On efface la valeur de la variable

$x:$

$-3x+2x=-3-1$

$-x=-4$

$x=4$

Et une fois qu’on sait combien ça vaut

$x,$ Nous substituons sa valeur dans l’une ou l’autre des équations pour trouver la valeur de $y:$

$y=-3x+1 \ \xrightarrow{x \ = \ 4} \ y=-3\cdot 4+1$

$y =-12+1$

$y =-11$

Les coordonnées du point d’intersection entre les deux lignes sont donc :

$\bm{(4,-11)}$

Exercice 3

Déterminez le point d’intersection ou l’intersection entre les deux lignes suivantes :

$\displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases} \qquad \qquad s: \ 4x+2y+8=0$

voir solution

Tout d’abord, nous devons savoir s’il s’agit de deux lignes parallèles ou non. Pour ce faire, nous allons voir si les vecteurs directeurs des deux droites sont proportionnels.

le droit

$r$ est défini sous la forme d’équations paramétriques, donc les composantes de son vecteur directeur sont les coefficients devant le paramètre $t:$

$\vv{r} =(2,-3)$

Et, d’autre part, la ligne

$s$ est décrit sous la forme d’une équation implicite, donc son vecteur directeur est :

$\vv{s} =(-B,A)=(-2,4)$

Pour que les composantes des deux vecteurs directeurs ne soient pas proportionnelles l’une à l’autre, les deux droites ne sont donc pas parallèles.

$\cfrac{2}{-2} \neq \cfrac{-3}{4} \ \longrightarrow \ r \ \cancel{\parallel} \ s$

Et puisque les deux droites ne sont pas parallèles, cela implique qu’il y a bien un point d’intersection entre elles. Pour le calculer, il faut résoudre le système d’équations formé par l’équation de chaque droite :

$\displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases} \qquad \qquad s: \ 4x+2y+8=0$

Dans ce cas, comme la ligne

$r$ est sous forme d’équations paramétriques, il faut substituer l’expression de chaque équation paramétrique dans l’équation de l’autre droite :

$4(1+2t)+2(-2-3t)+8=0$