Lignes coplanaires

Sur cette page, vous découvrirez ce que signifie que deux droites sont coplanaires. Vous pourrez également voir quand deux droites sont coplanaires et, en plus, vous trouverez des exemples et des exercices résolus de droites coplanaires.

Que sont deux droites coplanaires ?

En géométrie analytique, la définition des droites coplanaires est la suivante :

Deux droites sont coplanaires lorsqu’elles sont dans le même plan. Par conséquent, les lignes coplanaires ne peuvent être que des lignes sécantes , des lignes parallèles ou des lignes coïncidentes .

De plus, deux lignes coplanaires suffisent pour définir complètement un plan. Bien qu’évidemment un plan puisse avoir plus de deux droites coplanaires, en fait tout plan contient une infinité de droites.

D’autre part, si deux droites ne sont pas coplanaires, cela signifie qu’elles se coupent.

Exemples de lignes coplanaires

Afin que vous compreniez mieux la notion de droites coplanaires, voici un exemple avec trois droites :

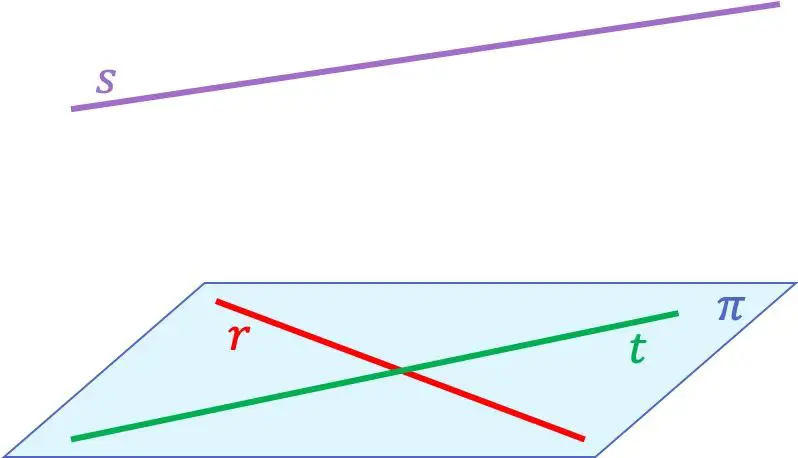
Dans ce cas, les lignes

et Ils sont coplanaires car ils appartiennent au même plan. Au lieu de cela, la ligne droite n’est coplanaire à aucune des deux autres droites, puisqu’elle coupe les droites et

Comment savoir si deux droites sont coplanaires ?

Comme nous l’avons vu plus haut dans l’explication des lignes coplanaires, celles-ci ne peuvent être que des lignes sécantes, parallèles ou coïncidentes. Autrement dit, 2 lignes croisées ne seront jamais coplanaires.

Par conséquent, pour savoir si deux lignes sont coplanaires, la position relative entre elles doit être déterminée, et s’il s’agit de deux lignes sécantes, parallèles ou coïncidentes, cela signifie qu’il s’agit de lignes coplanaires.

Ainsi, pour vérifier la coplanarité de deux droites, il faut d’abord savoir calculer la position relative de deux droites dans l’espace . Si vous ne maîtrisez toujours pas ce concept, il vaut mieux que vous regardiez d’abord le lien, où vous trouverez l’explication complète ainsi que des exemples, des exercices et des problèmes résolus.

Exercice résolu des droites coplanaires

A titre d’exemple, nous allons résoudre un exercice type sur les droites coplanaires :

• Déterminez si les deux droites suivantes sont coplanaires ou non :

La première chose que nous devons faire est de trouver la position relative entre les deux lignes et, pour cela, nous devons avoir les deux exprimées avec le même type d’équation. Alors nous passerons la ligne droite

de l’équation générale (ou implicite) aux équations paramétriques :

Donc le vecteur directeur de chaque droite est :

Les coordonnées des vecteurs directeurs des deux lignes sont proportionnelles, elles ne peuvent donc être que des lignes coïncidentes ou parallèles. Par conséquent, dans ce cas particulier, il n’est pas nécessaire de calculer la position relative exacte, puisque les lignes parallèles et les lignes coïncidentes sont des lignes coplanaires. Donc les deux droites sont coplanaires .