Sur cette page, vous trouverez une explication de ce qu’est un avion, comment il est calculé et toutes ses propriétés. De plus, vous pourrez voir des exemples de plans, quelles sont les positions relatives entre deux plans, comment déterminer l’angle entre 2 plans et, enfin, comment exprimer n’importe quel plan numériquement en utilisant les équations du plan.
Qu’est-ce qu’un plan ?
En géométrie analytique, la définition du plan est la suivante :
Un plan est un objet géométrique qui a deux dimensions (longueur et largeur).
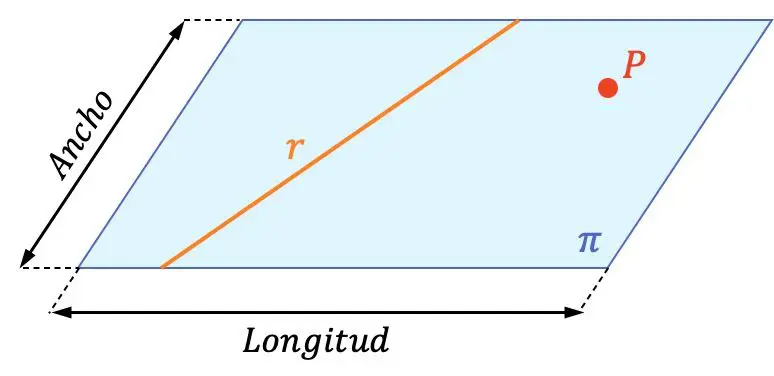
Par conséquent, un plan contient des lignes infinies et des points infinis. Dans la représentation graphique ci-dessus, vous pouvez voir la différence entre un plan, une ligne et un point. Vous pouvez également vérifier que la ligne
![]() et la pointe
et la pointe![]() sont contenus dans l’avion
sont contenus dans l’avion![]()
Comme vous pouvez le voir dans le plan représenté graphiquement, les plans sont généralement nommés avec des lettres grecques :
![]()
Un exemple de plan que nous utilisons beaucoup en mathématiques est le plan cartésien. Le plan cartésien est le plan défini par l’axe des abscisses (axe X) et l’axe des ordonnées (axe Y). L’une des utilisations du plan cartésien est qu’il est utilisé pour décrire la position d’un objet dans un système de référence.
Détermination d’un plan
Maintenant que nous avons vu la signification d’un plan, voyons comment n’importe quel plan dans l’espace tridimensionnel (dans R3) peut être déterminé.
Un plan est entièrement déterminé par les éléments géométriques suivants :
- Trois points non alignés.
- Une droite et un point à l’extérieur.
- Deux lignes parallèles ou deux lignes qui se croisent.
En ce qui concerne le dernier point, vous savez sûrement déjà ce que cela signifie que deux droites soient parallèles. Mais la signification des lignes sécantes est moins connue, donc si vous avez des questions ici, vous pouvez consulter ce que sont les lignes sécantes .
Par conséquent, si nous avons l’une des 3 conditions précédentes, cela signifie que nous pouvons former un plan.
propriétés du plan
Le plan répond aux caractéristiques suivantes :
- Un plan contient une infinité de points.
- Un plan contient une infinité de droites.
- Un plan est illimité, c’est-à-dire qu’il s’agit d’une surface qui s’étend dans l’espace sans limites.
- Deux plans sécants déterminent une ligne.
- Une droite qui a un point dans un plan n’y est pas nécessairement contenue. Pour qu’une droite fasse partie d’un plan, elle doit avoir au moins deux points dans le plan.
- Des plans infinis traversent une ligne droite.
- Un demi-plan est chacune des 2 parties en lesquelles un plan est divisé lorsqu’il est coupé par l’une de ses lignes.
équations planes
En géométrie analytique, l’ équation d’un plan est une équation qui permet d’exprimer mathématiquement n’importe quel plan. Donc, pour trouver l’équation d’un plan, vous n’avez besoin que d’un point et de deux vecteurs linéairement indépendants appartenant à ce plan.

Cependant, comme nous l’avons vu plus haut dans l’explication de la notion de plan, il existe plusieurs manières de déterminer un plan. Eh bien, de la même manière, il existe également différentes manières d’exprimer analytiquement un plan.
Ainsi tous les types d’équations du plan sont : l’ équation vectorielle , les équations paramétriques , l’ équation implicite (ou générale) et l’ équation canonique (ou segmentaire) du plan.
Ensuite nous allons voir en détail l’explication et la formule de toutes les équations du plan.
Équation vectorielle du plan
Soit un point et deux vecteurs directeurs d’un plan :
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
La formule de l’équation vectorielle d’un plan est :
![]()
Ou équivalent:
![]()
Où
![]() et
et![]() sont deux scalaires, c’est-à-dire deux nombres réels.
sont deux scalaires, c’est-à-dire deux nombres réels.
Équations paramétriques du plan
La formule de l’ équation paramétrique d’un plan est la suivante :
![]()
Où:
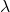 et
et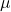 sont deux scalaires, c’est-à-dire deux nombres réels.
sont deux scalaires, c’est-à-dire deux nombres réels.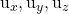 sont les composantes de l’un des deux vecteurs directeurs du plan
sont les composantes de l’un des deux vecteurs directeurs du plan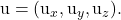
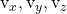 sont les composantes de l’autre vecteur directeur du plan
sont les composantes de l’autre vecteur directeur du plan 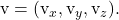
Équation implicite ou générale du plan
Soit un point et deux vecteurs directeurs d’un plan :
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
L’équation implicite, générale ou cartésienne d’un plan s’obtient en résolvant le déterminant suivant et en fixant le résultat égal à 0 :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Ainsi, l’ équation implicite ou générale du plan résultant sera la suivante :
![]()
Ce type d’équation du plan est aussi appelé équation cartésienne du plan.
Équation canonique ou segmentaire du plan
La formule de l’équation canonique ou segmentaire d’un plan est la suivante :
![]()
Où:
 est le point d’intersection entre le plan et l’axe X.
est le point d’intersection entre le plan et l’axe X. est le point d’intersection entre le plan et l’axe Y.
est le point d’intersection entre le plan et l’axe Y. C’est là que le plan coupe l’axe Z.
C’est là que le plan coupe l’axe Z.
L’équation canonique (ou équation segmentaire) du plan peut également être obtenue à partir de son équation générale :
![]()
Tout d’abord, nous résolvons le coefficient D de l’équation :
![]()
Puis on divise l’équation entière du plan par la valeur du paramètre D changé de signe :
![]()
![]()
Et, en utilisant les propriétés des fractions, nous arrivons à l’expression suivante :
![]()
On déduit donc de cette expression les formules permettant de calculer directement les termes de l’équation canonique ou segmentaire d’un plan :
![]()
Par conséquent, pour pouvoir former cette variante des équations du plan, il faut que les coefficients A, B et C soient différents de zéro, évitant ainsi les indéterminations des fractions.
Position relative de deux plans
En géométrie analytique, il n’y a que trois positions relatives possibles entre deux plans : plans sécants, plans parallèles et plans coïncidents.
- Plans sécants : Deux plans sont sécants s’ils ne se coupent que sur une ligne.
- Plans parallèles : Deux plans sont parallèles s’ils ne se coupent en aucun point.
- Plans coïncidents : Deux plans sont coïncidents s’ils ont tous des points en commun.
plans sécants

plans parallèles

avions coïncidents

De plus, si deux plans sécants se coupent à un angle de 90º, ce sont deux plans mutuellement perpendiculaires .
Angle entre deux plans
L’angle entre deux plans est égal à l’angle formé par les vecteurs normaux desdits plans. Par conséquent, pour trouver l’angle entre deux plans, l’angle formé par leurs vecteurs normaux est calculé, car ils sont équivalents.
Alors, une fois que l’on sait exactement en quoi consiste l’angle entre deux plans, voyons la formule pour calculer l’angle entre deux plans dans l’espace, qui se déduit de la formule de l’angle entre deux vecteurs :
Étant donné l’équation générale (ou implicite) de deux plans différents :
![]()
![]()
Le vecteur normal de chaque plan est :
![]()
![]()
Et l’angle formé par ces deux plans est déterminé en calculant l’angle formé par leurs vecteurs normaux à l’aide de la formule suivante :
![]()
Évidemment, une fois que l’on a calculé le cosinus de l’angle formé par les deux plans à partir de la formule, il faut inverser le cosinus pour trouver la valeur dudit angle.
Par contre, lorsque les deux plans sont perpendiculaires ou parallèles, il n’est pas nécessaire d’appliquer la formule, car l’angle entre les 2 plans peut être déterminé directement :
- L’angle entre deux plans parallèles est de 0º, puisque leurs vecteurs normaux ont la même direction.
- L’angle entre deux plans perpendiculaires est de 90º, car leurs vecteurs normaux sont également perpendiculaires (ou orthogonaux) l’un à l’autre et forment donc un angle droit.