Que sont les vecteurs (mathématiques) ?

Sur cette page, vous trouverez tout sur les vecteurs : ce qu’ils sont, leurs caractéristiques, comment ils sont calculés, comment faire des opérations avec des vecteurs, les différents types qui existent,…

Qu’est-ce qu’un vecteur ?

La définition mathématique d’un vecteur est la suivante :

En mathématiques, un vecteur est un segment orienté qui va d’un point (appelé l’origine) à un autre point (appelé la fin).

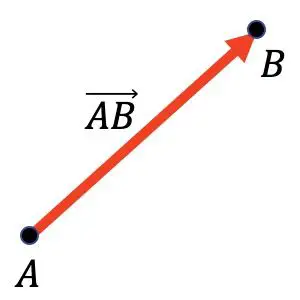
Par exemple, dans la représentation graphique ci-dessous, vous pouvez voir que le vecteur

$\vv{AB}$ Il a le point A comme origine et le point B comme point final.

Les vecteurs sont principalement utilisés en mathématiques, en particulier en géométrie, et en physique, pour représenter graphiquement les forces vectorielles.

Caractéristiques d’un vecteur

Une fois que nous avons vu quelle est la signification mathématique des vecteurs, voyons maintenant quelles sont leurs propriétés.

Chaque vecteur a les caractéristiques géométriques suivantes :

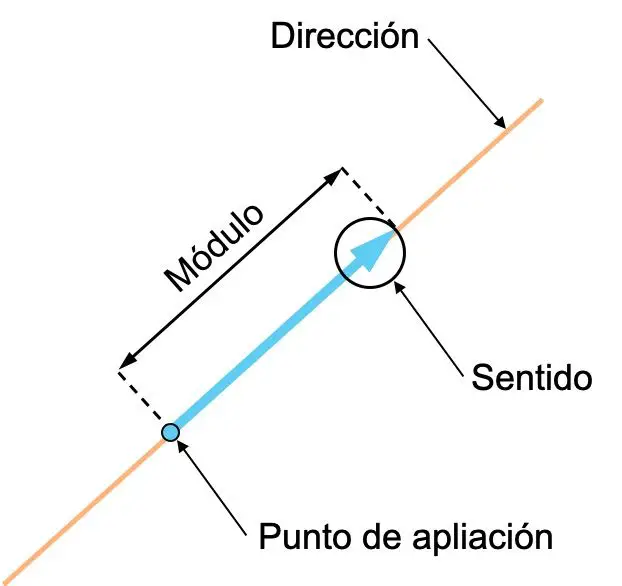
Direction : La direction d’un vecteur correspond à la direction de la ligne qui contient le vecteur ou de toute ligne parallèle à celui-ci. En d’autres termes, la direction d’un vecteur est la droite sur laquelle il se trouve.
Direction : la direction d’un vecteur est l’orientation dudit vecteur, indiquée par sa flèche.
Module (ou magnitude) : le module d’un vecteur est sa longueur, et correspond à la valeur numérique du vecteur. Par conséquent, plus le vecteur signifie grand, plus la quantité vectorielle qu’il représente est grande.
Point d’application : le point d’application d’un vecteur est l’origine dudit vecteur.

caractéristiques géométriques des vecteurs

Les notions de direction et de sens d’un vecteur prêtent souvent à confusion, il est donc important de distinguer la différence entre elles. Regardez l’exemple suivant avec deux vecteurs, les deux ont la même direction mais leurs sens sont différents :

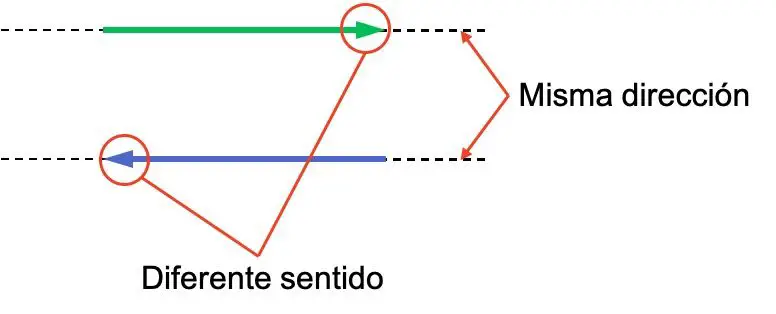
signification du sens et de la direction d'un vecteur

Les deux vecteurs ont la même direction car ils sont parallèles. Au lieu de cela, leurs sens sont opposés car ils sont tournés vers l’arrière.

Composants d’un vecteur

Nous venons de voir que les vecteurs sont représentés graphiquement par des flèches, mais les vecteurs peuvent aussi être représentés numériquement par les composantes (ou coordonnées) d’un vecteur.

Par exemple, si nous avons le vecteur suivant représenté dans un graphique :

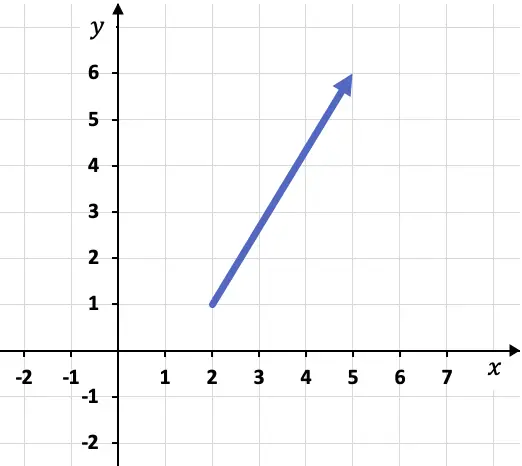
Pour calculer les composantes du vecteur, nous devons d’abord identifier les coordonnées de son origine et de sa fin, c’est-à-dire les points où il commence et où il se termine. Dans ce cas, l’origine et la fin du vecteur sont :

Origine du vecteur : A(2,1)

Point final du vecteur : B(5,6)

Ainsi, pour trouver les coordonnées ou les composantes du vecteur, il suffit de soustraire le point final moins l’origine :

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

De sorte que les composantes du vecteur représenté dans le graphique sont :

$\vv{\bm{AB}}\bm{=(3,5)}$

Opérations vectorielles

ajout de vecteur

Pour additionner numériquement deux vecteurs, vous devez additionner leurs composantes respectives. Ou en d’autres termes, les coordonnées X des deux vecteurs sont additionnées et identiques aux coordonnées Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

Pour que vous puissiez voir comment cela se fait, nous allons ajouter les deux vecteurs suivants :

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

Deux vecteurs peuvent également être ajoutés à partir de leurs représentations graphiques. Pour cela, la règle ou la loi du parallélogramme est normalement utilisée, mais il existe de nombreuses méthodes. Vous pouvez voir des exemples et des exercices résolus sur la façon d’ajouter graphiquement deux vecteurs ici.

soustraction vectorielle

Pour soustraire deux vecteurs analytiquement, vous devez soustraire leurs composantes respectives. C’est-à-dire que les coordonnées X des deux vecteurs sont soustraites l’une de l’autre et identiques aux coordonnées Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

A titre d’exemple, nous allons soustraire les deux vecteurs suivants :

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

Comme pour l’addition, vous pouvez également soustraire 2 vecteurs en utilisant leurs représentations. Pour cela, la règle ou la loi du triangle est généralement utilisée, mais il existe plusieurs méthodes. Vous pouvez les voir tous avec des exemples et des exercices résolus sur la façon de soustraire deux vecteurs graphiquement .

module d’un vecteur

Comme nous l’avons vu au début de cette page, la magnitude d’un vecteur correspond à la longueur de ce vecteur. Eh bien, la longueur (ou l’ampleur) d’un vecteur peut être déterminée à partir de ses composants.

Soit n’importe quel vecteur :

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Pour trouver la magnitude d’un vecteur dans le plan, il faut appliquer la formule suivante :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

Par exemple, nous allons calculer la magnitude du vecteur suivant à l’aide de la formule :

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

Bien que cela semble très simple, déterminer la magnitude d’un vecteur peut être compliqué. Si vous voulez voir plus d’exemples et pratiquer avec des exercices résolus du module d’un vecteur , nous vous recommandons de visiter cette page liée.

Multiplication d’un vecteur par un scalaire

Pour calculer numériquement le produit d’un vecteur par un nombre (ou un scalaire), chaque composante du vecteur doit être multipliée par ce nombre.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

Dans l’exemple générique suivant, vous pouvez voir comment la direction du vecteur est maintenue quel que soit le signe du scalaire. Par contre, le sens du vecteur dépend du signe du nombre qu’il multiplie.

multiplication ou produit d'un nombre ou d'un scalaire par un vecteur

Ci-dessous, vous pouvez voir un exemple numérique de la façon de trouver le produit d’un vecteur et d’un nombre :

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

Produit scalaire

En géométrie analytique, le produit scalaire est une opération vectorielle qui multiplie deux vecteurs et les transforme en un nombre réel.

Ainsi, la formule du produit scalaire de deux vecteurs est la suivante :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

Ci-dessous vous avez un exemple où le résultat du produit scalaire entre deux vecteurs est calculé :

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

Dans ce lien, vous pouvez voir plus d’exemples du produit scalaire . De plus, vous y trouverez une autre façon de trouver le produit scalaire entre deux vecteurs, les propriétés de ce type d’opération avec des vecteurs et des exercices résolus pas à pas.

produit vectoriel

Bien que leur nom soit très similaire, le produit scalaire et le produit croisé sont complètement différents.

Le produit croisé , également appelé produit croisé, est une opération entre deux vecteurs dans l’espace (dans R3), c’est-à-dire qu’il s’agit de vecteurs à trois coordonnées.

Donc, si nous avons deux vecteurs tridimensionnels quelconques :

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Le produit vectoriel des deux vecteurs est égal au résultat du déterminant 3×3 suivant :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

où les vecteurs

$\vv{i}, \vv{j},\vv{k}$ sont les vecteurs unitaires dans les directions des axes X, Y, Z respectivement.

De plus, la direction du vecteur résultant est perpendiculaire aux deux vecteurs multipliés.

Comme vous pouvez le deviner, résoudre ce type d’opération est plus difficile que les précédents et, pour cette raison, nous avons une page entière avec une explication détaillée de la façon dont le produit vectoriel entre deux vecteurs est calculé. Par conséquent, si vous êtes intéressé, nous vous recommandons de le visiter et de vous entraîner avec les exercices résolus du produit vectoriel .

produit mélangé

Le produit mixte de trois vecteurs, également appelé triple produit scalaire, est une multiplication successive entre trois vecteurs impliquant deux types d’opérations différentes : le produit scalaire et le produit vectoriel. Ainsi, la combinaison des deux opérations vectorielles donne un scalaire (un nombre réel).

Concrètement, le produit mixte consiste à calculer le produit vectoriel de deux vecteurs et, ultérieurement, à multiplier vectoriellement le résultat obtenu par un troisième vecteur. Regarde la formule :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

Comme pour le produit vectoriel, résoudre le produit mixte entre vecteurs n’est pas facile. Pour cette raison, nous vous recommandons de jeter un œil à cette explication du produit mixte de trois vecteurs , où vous trouverez des exemples, des exercices résolus et la signification géométrique de cette opération vectorielle.

types de vecteurs

Il existe de nombreux types de vecteurs différents, mais les définitions les plus importantes à connaître sont les suivantes :

Vecteur unitaire : vecteur dont le module est égal à 1.
Vecteur fixe : Un vecteur est fixe lorsque l’origine du vecteur est appliquée à un point fixe.
Vecteur libre : Un vecteur est libre lorsque son point d’application n’est pas défini, mais est un point libre.
Vecteurs colinéaires : deux ou plusieurs vecteurs sont colinéaires s’ils partagent la même ligne d’action (ligne où se trouve le vecteur).
Vecteurs équivalents : deux vecteurs sont équipollens s’ils ont même grandeur, même sens et même direction (bien qu’ils puissent avoir des points d’application différents).
Vecteurs liés : Les vecteurs liés sont des vecteurs équipollens qui agissent également sur la même ligne.
Vecteurs opposés : deux vecteurs sont opposés s’ils ont la même grandeur et la même direction mais un sens différent.
Vecteur position : le vecteur position est le vecteur dont l’origine est le point (0,0) (origine des coordonnées).
Vecteurs concurrents : deux ou plusieurs vecteurs sont concurrents lorsque leurs lignes d’action passent par le même point, c’est-à-dire qu’elles se croisent.
Vecteurs parallèles : deux ou plusieurs vecteurs sont parallèles s’ils ont la même direction, quels que soient leurs sens.
Vecteurs perpendiculaires : Deux vecteurs sont perpendiculaires (ou orthogonaux) lorsque leurs directions forment un angle de 90º.
Vecteurs orthonormés : Deux ou plusieurs vecteurs sont orthonormés s’ils sont perpendiculaires l’un à l’autre et, de plus, ils sont unitaires (leur grandeur est égale à l’unité).
Vecteurs coplanaires : deux ou plusieurs vecteurs sont coplanaires lorsqu’ils sont contenus dans le même plan.

Angle entre deux vecteurs

Pour trouver l’angle entre deux vecteurs donnés, il faut appliquer la formule suivante :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$